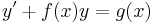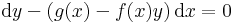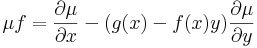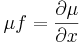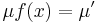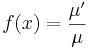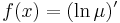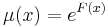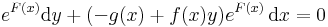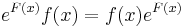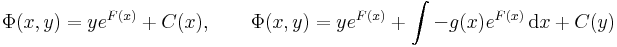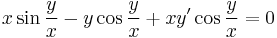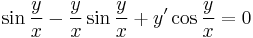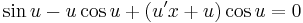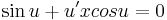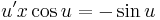Matematika A3a 2008/3. gyakorlat
Tartalomjegyzék |
Integráló tényező
Általában egy P(x,y)dx+Q(x,y)dy=0 alakú differenciálegyenlet esetén nem teljesül a rot(P,Q)=0 feltétel. Esetenként azonban található olyan μ kétváltozós pozitív értékű függvény, amellyel:
már egzakt egyenlet. Vizsáljuk meg miből nyerhetjük az ilyen μ un. integráló szorzót! A rot(μP,μQ)=0 feltétel a következő:
Mivel
és ugyanígy
ezért
Ezt a parciális differenciálegyenletet kell megoldanunk ahhoz, hogy legyen integráló tényezőnk.
Speciális esetek
Megállapíthatjuk, hogy néha érdemes a μ-re felírt egyenletnek csak olyan megoldásait keresni, amelyek csak az egyik változótól függenek. Ez a következő esekben áll elő.
I. Keressük a megoldást a μ=μ(x) feltevéssel! Ekkor ln(μ)=ln(μ)(x) és ∂yln(μ)=0, azaz
és
csak x-től függ és innen az integráló szorzó:
Példa.
Az x>0, y tetszőleges kezdeti érték tarrtományban oldjuk meg az alábbi egyenletet!
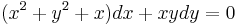 , (xyy' = − x2 − y2 − x)
, (xyy' = − x2 − y2 − x)
Mo. P = x2 + y2 + x, Q = xy, 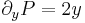 ,
, 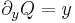 azaz nem egzakt, de
azaz nem egzakt, de
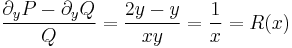 ,
, 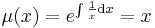
II. Keressük a megoldást a μ=μ(y) feltevéssel! Ekkor ln(μ)=ln(μ)(y) és ∂xln(μ)=0, azaz
és
csak y-től függ és innen az integráló szorzó:
Megj.: A gyakorlatban ilyenkor vesszük az
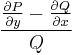 ill.
ill. 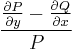
törteket és ellenőrizzük, hogy rendre csak x-től vagy csak y-tól függenek. Ha valamelyik, akkor azt a megoldást választjuk.
Példa.
Oldjuk meg az
egyenletet!
1. Mo. Nem egzakt:
Egzakttá tehető, ugyanis:
Emiatt
Megoldása:
2. Mo. Szeparábilis is.
III. Előfordulhat, hogy szeparábilis alakban kell keresnünk a parc. diff. egyenlet megoldását, azaz μ(x,y)=φ(x)ψ(y) alakban. Ekkor -- mint az könnyen ellenőrizhető -- az egyenlet
alakú és az integráló szorzó
Példa. Oldjuk meg az
egyenletet!
Mo. Átrendezve:
∂yP=3y2, ∂xQ=-y2, azaz
azaz célravezet, ha μ-t μ(x) alakban keressük. Ekkor
Ekkor az egyenlet:
egzakt, mert
Integrálássa:
azaz
Elméleti példák
1. Az y'=-P/Q homogén fokszámú egyenlet, melyben P és Q azonos fokszámú homogén függvények szintén egzakttá tehető az 1/(Px+Qy) szorzóval, ha ez nem az y'=-y/x egyenlet (ennek meg ismerjük a megoldását).
2. Keressünk integráló tényezőt az
közönséges elsőrendű inhomogén lineáris differenciálegyenlethez!
Világos, hogy nem egzakt, mert a
alakban a keresztben vett deriváltak: 0 és f(x).
Q=1 és P(x,y)=-g(x)+f(x)y ezért a μ-t adó parc.diff. egyenlet:
Elegendő egy partikuláris megoldást találni, amit egyszerűen megkapunk, ha csak az olyan μ-ket keressük, amik csak az x-től függenek, ekkor ugyanis pl. g(x) nem is lesz az egyenletben. Ilyet találunk, mert:
Ez egy szeparábilis, aminek a megoldása:
egy partikuláris megoldás:
ahol F'=f.
HF: Keressük meg ezzel az integáló szorzóval az általános megoldást!
Mo.
Már egzakt, hiszen
Ekkor
azaz
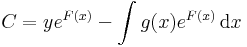
Gyakorlás
Oldja meg az alábbi egyenletet az a) y(π)=0 ill. b) y(2/π)=1 kezdeti feltétel mellett!
Mo. Legyen u = y / x, innen y' = u'x + u
(itt megjegyzendő, hogy az u=kπ konstansok megoldások, azaz az eredetinek az y=kπx megoldásai)
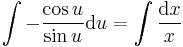
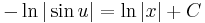
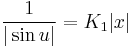
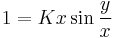 (K≠0)
(K≠0)
Függvényegyütthatós elsőrendű lineáris d.e.
Mo. Homogén megoldása. y=0 konstans megoldás.
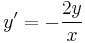
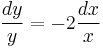
- ln | y | = ln | x | − 2 + C
Bolzano tétele miatt tetszőleges K valós számmal:
ami a homogén általános megoldása.
Inhomogén part. keresése
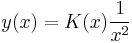
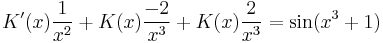
- K'(x) = x2sin(x3 + 1)
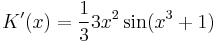
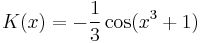
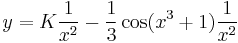
| 2. gyakorlat |
| 4. gyakorlat |
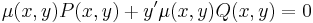
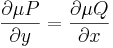
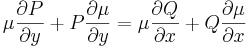
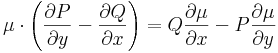
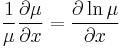
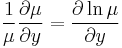
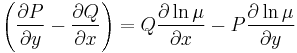
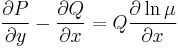
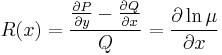
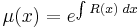
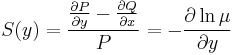
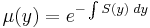
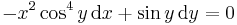
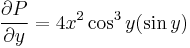
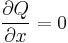
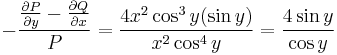
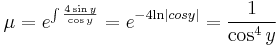
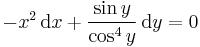
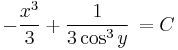
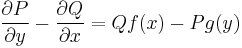
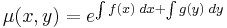
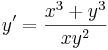
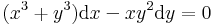
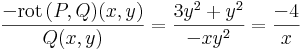
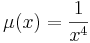
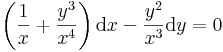
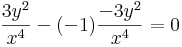
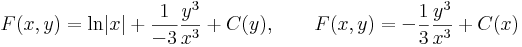
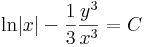
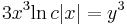
![x\sqrt[3]{3\,\mathrm{ln}\,c|x|}=y(x)\,](/upload/math/d/d/0/dd047c99fd5100a705896f6427be4de3.png)