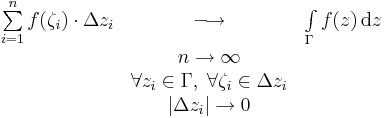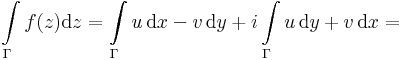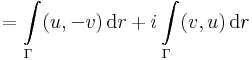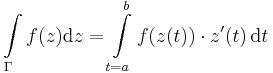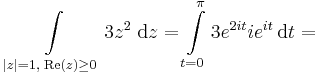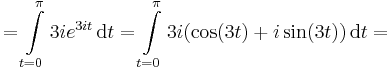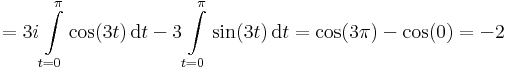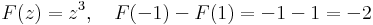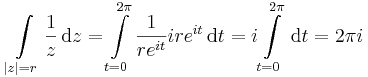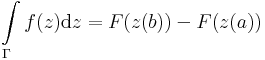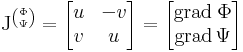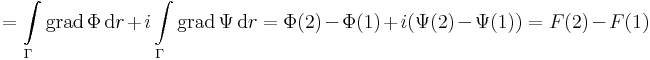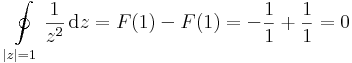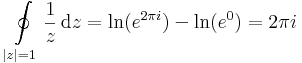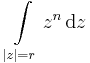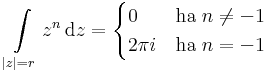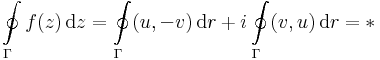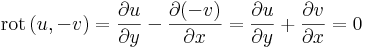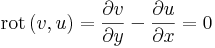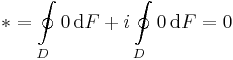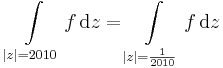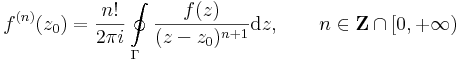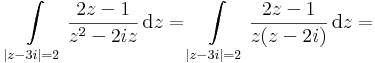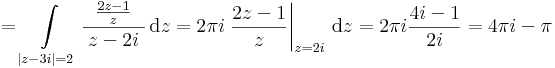Matematika A3a 2009/7. gyakorlat

Komplex integrál

A komplex integrálás egy bizonyos pontig szoros párhuzamot mutat az R²-re vonatkozó integráltételekkel. Azonban Goursat eredményét figyelembe véve kiderül, hogy a nyílt halmazon értelmezett komplex differenciálható függvények egyetéen differenciálhatósági osztályt alkotnak (a valósokkal szemben), éspedig az analitikust, amit ezesetben regulárisnak neveznek.

Definíció szerint, ha f: D $\to$ C egy nyílt tartományon értelmezett függvény és Γ:[a,b] $\to$ C folytonosan differenciálható görbe, akkor a f integrálja a Γ mentén:

$\begin{matrix} \sum\limits_{i=1}^nf(\zeta_i)\cdot \Delta z_i & \longrightarrow & \int\limits_{\Gamma}f(z)\,\mathrm{d}z\\ & n\to \infty & \\ & \forall z_i\in \Gamma, \;\forall \zeta_i\in \Delta z_i &\\ & |\Delta z_i|\to 0 & \end{matrix}$

Fontos, hogy a fenti definícióban az f(z) Δz egy komplex szorzat.

Persze itt olyan fogalmakkal dolgozunk, amelyeket nyugodtan átfogalmazhatunk egy vonalintegrál párrá, a következőképpen. Tekintsük az f = u + v i függvényt és a dz = dx + i dy szimbólumot. Ekkort fdz komplex formális szorzát elvégezve kapjuk, hogy:

$\int\limits_{\Gamma}f(z)\mathrm{d}z = \int\limits_{\Gamma} u\,\mathrm{d}x-v\,\mathrm{d }y + i\int\limits_{\Gamma} u\,\mathrm{d}y+v\,\mathrm{d }x=$

$=\int\limits_{\Gamma}(u,-v)\,\mathrm{d}r+i\int\limits_{\Gamma}(v,u)\,\mathrm{d}r$

Integrál kiszámítása paraméteresen

A vonalintegál kiszámítására vonatkozó formula komplex változata az lesz, hogy:

$\int\limits_{\Gamma}f(z)\mathrm{d}z=\int\limits_{t=a}^{b}f(z(t))\cdot z'(t)\,\mathrm{d}t$

Itt z(t)=Γ(t). De így ritkán számolunk komplex integrált.

1. Feladat. r>0

a) $\int\limits_{|z|=1,\;\mathrm{Re}(z)\geq 0}3z^2\;\mathrm{d}z=?$

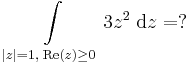
b) $\int\limits_{|z|=r}\frac{1}{z}\,\mathrm{d}z=?$

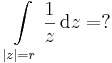
Mo.

$\int\limits_{|z|=1,\;\mathrm{Re}(z)\geq 0}3z^2\;\mathrm{d}z=\int\limits_{t=0}^{\pi}3e^{2it}ie^{it}\,\mathrm{d}t=$

hiszen a paraméterezés z(t)=e^it, t ∈ [0,π]. Egy vektorértékű valós változós függvényt komponensenként integrálunk:

$=\int\limits_{t=0}^{\pi}3ie^{3it}\,\mathrm{d}t=\int\limits_{t=0}^{\pi}3i(\cos(3t)+i\sin(3t))\,\mathrm{d}t=$

$=3i\int\limits_{t=0}^{\pi}\cos(3t)\,\mathrm{d}t-3\int\limits_{t=0}^{\pi}\sin(3t)\,\mathrm{d}t=\cos(3\pi)-\cos(0)=-2$

2. Mo. Szerencsére a komplex analízisben van is van Newton--Leibniz formula:

$F(z)=z^3,\quad F(-1)-F(1)=-1-1=-2$

b)

$\int\limits_{|z|=r}\frac{1}{z}\,\mathrm{d}z=\int\limits_{t=0}^{2\pi}\frac{1}{re^{it}}ire^{it}\,\mathrm{d}t=i\int\limits_{t=0}^{2\pi}\,\mathrm{d}t=2\pi i$

Newton--Leibniz-tétel

R² vektorfüggvényeinek integrálása könnyen elvégezhető, ha feltesszük hogy az integrandusnak van potenciálja. Ekkor az első gradiens tételre kell hivatkoznunk. Komplex esetben ez az összefüggés a valós N--L-formula alakját ölti.

Tétel (Newton--Leibniz) Ha f: D $\to$ C folytonos a D nyílt halmazon és létezik primitív függvénye, akkor minden a D-ben haladó Γ[a,b] $\to$ C görére:

$\int\limits_{\Gamma}f(z)\mathrm{d}z=F(z(b))-F(z(a))$

ahol Γ kezdő és végpontja z(a) és z(b).

2. Feladat. Igazoljuk a N--L-tételt!.

Mo. Tegyük fel, hogy F'=f és legyen F = (Φ,Ψ), f=(u,v). Ekkor F deriváltja azonosítható a (Φ,Ψ) vektorfüggvény Jacobi-mátrixával, ami a feltevés szerint folytonos és egyenlő f=(u,v) mátrixalakjával.

$\mathrm{J}^{\Phi \choose \Psi}=\begin{bmatrix}u & -v \\ v & u\end{bmatrix}=\begin{bmatrix}\mathrm{grad}\;\Phi \\ \mathrm{grad}\,\Psi\end{bmatrix}$

Mindkét komponensre felírhatjuk tehát az első gadiens tételt, és kapjuk: $\int\limits_{\Gamma}f(z)\mathrm{d}z=\int\limits_{\Gamma}(u,-v)\,\mathrm{d}r+i\int\limits_{\Gamma}(v,u)\mathrm{d}r=$

$=\int\limits_{\Gamma}\mathrm{grad}\,\Phi\,\mathrm{d}r+i\int\limits_{\Gamma}\mathrm{grad}\,\Psi\,\mathrm{d}r=\Phi(2)-\Phi(1)+i(\Psi(2)-\Psi(1))=F(2)-F(1)$

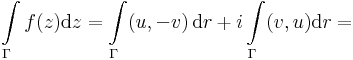
3. Feladat.

a) $\oint\limits_{|z|=1}\frac{1}{z^2}\,\mathrm{d}z=?$

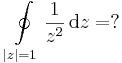
b) $\oint\limits_{|z|=1} \frac{1}{z}\,\mathrm{d}z=?$

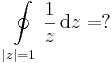
Mo. a)

$\oint\limits_{|z|=1}\frac{1}{z^2}\,\mathrm{d}z=F(1)-F(1)=-\frac{1}{1}+\frac{1}{1}=0$

hiszen F(z)=-1/z-vel F'=f.

b)

$\oint\limits_{|z|=1} \frac{1}{z}\,\mathrm{d}z=\mathrm{ln}(e^{2\pi i})-\mathrm{ln}(e^{0})=2\pi i\,$

ahol ln 1-et kétféleképpen, egyfelől az első, másfelől a második Riemann-levélen számoltuk ki. A logaritmus Riemann-felületén a logaritmus ugyanis már egyértékű.

4. Feladat Legyen n ∈ Z, r>0. Mennyi:

$\int\limits_{|z|=r}z^n\,\mathrm{d}z$

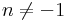Mo.$n\ne -1$-re létezik primitívfüggvény, ezért

$\int\limits_{|z|=r}z^n\,\mathrm{d}z=\begin{cases}0 & \mathrm{ha}\;n\ne -1\\2\pi i & \mathrm{ha}\;n=-1\end{cases}$

Cauchy-tétel

A síkon a Stokes- és a Gauss-tétel közül elegendő csak az egyiket ismernünk, mert igazolható, hogy az egyik tétel átfogalmazható a másikba (lásd Serény György: Formális és személetes vektoranalízis). A rotáció és a divergencia ugyan különböznek egymástól, de szintén igazolható, hogy bizonyos értelemben egymással azonosíthatóak.

Legyen f reguláris az egyszeresen összefüggő U tartományon és legyen Γ tetszőleges egyszerű, zárt görbe D ⊆ U határa. Írjuk fel a Stokes-tételt!

$\oint\limits_{\Gamma} f(z)\,\mathrm{d}z=\oint\limits_{\Gamma} (u,-v) \,\mathrm{d}r+i\oint\limits_{\Gamma} (v,u) \,\mathrm{d}r=*$

$\mathrm{rot}\,(u,-v)= \frac{\partial u}{\partial y}-\frac{\partial (-v)}{\partial x}=\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}=0$

$\mathrm{rot}\,(v,u)= \frac{\partial v}{\partial y}-\frac{\partial u}{\partial x}=0$

$*=\oint\limits_{D} 0\,\mathrm{d}F+i\oint\limits_{D} 0 \,\mathrm{d}F=0$

A meglepő, hogy a Goursat-tétel miatt ez a tétel akkor is igaz, ha f-ről nem tesszük fel azt, amit a Stokes-tétel, azaz hogy folytonosan differenciálható.

5. Feladat. Legyen f:C $\to$ C mindenhol reguláris kivéve az x₀=0 pontban. Igazoljuk, hogy ekkor

$\int\limits_{|z|=2010}f\,\mathrm{d}z=\int\limits_{|z|=\frac{1}{2010}}f\,\mathrm{d}z$

Cauchy-típusú integrálok

Reguláris f-re és egyszerű Γ görbére:

$f^{(n)}(z_0)=\frac{n!}{2\pi i}\oint\limits_{\Gamma}\frac{f(z)}{(z-z_0)^{n+1}}\mathrm{d}z,\quad\quad n\in\mathbf{Z}\cap[0,+\infty)$

6. Feladat.

(a) $\int\limits_{|z-3i|=2}\frac{2z-1}{z^2-2iz}\,\mathrm{d}z=?$

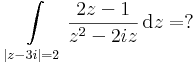
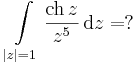
(b) $\int\limits_{|z|=1}\frac{\mathrm{ch}\,z}{z^5}\,\mathrm{d}z=?$

(c) $\int\limits_{|z|=2}\frac{\sin\,z}{z^2+1}\,\mathrm{d}z=?$

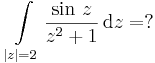
Mo. (a)

$\int\limits_{|z-3i|=2}\frac{2z-1}{z^2-2iz}\,\mathrm{d}z=\int\limits_{|z-3i|=2}\frac{2z-1}{z(z-2i)}\,\mathrm{d}z=$

a 0 kívül esik a körön, ezért a körön belül az f(z) = 2z-1/z reguláris, ezért az integrált előállítja a 2πif(z₀), ahol z₀=2i

$=\int\limits_{|z-3i|=2}\frac{\frac{2z-1}{z}}{\;z-2i\;}\,\mathrm{d}z=2\pi i\left.\frac{2z-1}{z}\right|_{z=2i}\,\mathrm{d}z=2\pi i\frac{4i-1}{2i}=4\pi i- \pi$

(b)

$\int\limits_{|z|=1}\frac{\mathrm{ch}\,z}{z^5}\,\mathrm{d}z=\frac{2\pi i}{4!}\mathrm{ch}^{(4)}(0)=\frac{\pi i}{12}$

(c)

$\int\limits_{|z|=2}\frac{\sin\,z}{z^2+1}\,\mathrm{d}z=\int\limits_{|z+i|=1/2}\frac{\frac{\sin z}{z-i}}{z+i}\,\mathrm{d}z+\int\limits_{|z-i|=1/2}\frac{\frac{\sin z}{z+i}}{z-i}\,\mathrm{d}z$

$=2\pi i\frac{\sin(-i)}{-2i}+2\pi i\frac{\sin(i)}{2i}=2\pi i\sin i=\pi(e+\frac{1}{e})$