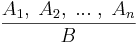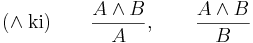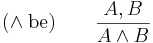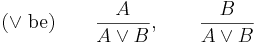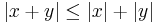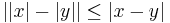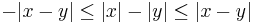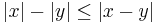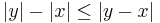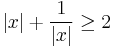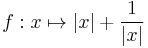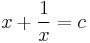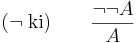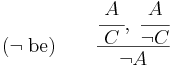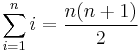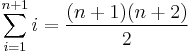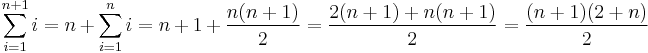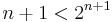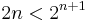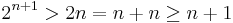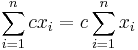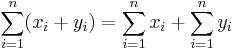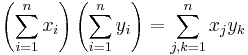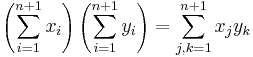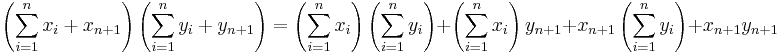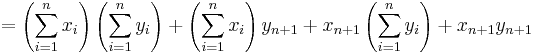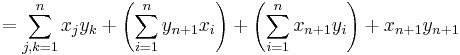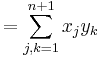Matematika közlek A1a 2013/1. gyakorlat
- Lásd még: Matematika közlek A1a 2013
Tartalomjegyzék |
Logikai következtetési sémák
Ha A1, A2, ..., An, B mondatok, akkor azt mondjuk, hogy az
szimbólummal jelölt következtetés helyes, ha minden olyan esetben, amikor az A1, A2, ..., An mondatok (az úgy nevezett premisszák vagy feltételek) mindegyike igaz, akkor a B mondat, azaz a konkúzió (következmény) is igaz.
A helyes következtetések listája elég nagy, ám vannak bizonyos tekintetben alapvetőnek tekinthető kövekeztetések, melyeket könnyen lehet kategorizálni a bevezetési és kiküszöbölési szabályok módszere szerint.
Direkt következtetések
A legegyszerűbb eset az és (jelben 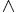 ) mondatoperátorral összekötött összetett mondatokra vonatkozó bevezetési és kiküszöbölési szabály. Egy mondatoperátor kiküszöbölési szabálya lényegében az, hogy megadja, mire következtethetünk az adott operátorral összekötött mondatokból, jelen esetben például A és B összetett mondatból. Eszerint:
) mondatoperátorral összekötött összetett mondatokra vonatkozó bevezetési és kiküszöbölési szabály. Egy mondatoperátor kiküszöbölési szabálya lényegében az, hogy megadja, mire következtethetünk az adott operátorral összekötött mondatokból, jelen esetben például A és B összetett mondatból. Eszerint:
Azaz, ha tudjuk, hogy A és B igaz, akkor jogos kijelentenünk, akár A, akár B igazságának fennállását. A bevezetési szabály azt adja meg, hogy miből következtethetünk az adott összetételre. Világos, hogy a helyes következtetés fenti értelemezése szerint minden olyan esetben, amikor az {A, B} premisszapár minden tagja igaz, levonhatjuk az A és B konklúziót:
A vagy (jelben: 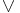 ) bevezetési szabálya szintén nyilvánvaló:
) bevezetési szabálya szintén nyilvánvaló:
Ezzel szemben a kiküszöbölési szabályának tárgyalásával máris belefutottunk a logikafilozófia ingoványába, ezt persze nem tárgyaljuk, csak magát a következtetési szabályt. A vagy kiküszöbölési szabályát az esetszétválasztás szabályának nevezzük:
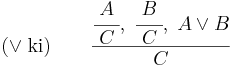 az esetszétválasztás szabálya
az esetszétválasztás szabálya
Azaz ha A-ból következik a C és a B-ből is következik a C, továbbá az A és a B közül legalább az egyik igaz (ez a klasszikus vagy: nem feltétlenül tudjuk, melyik igaz, csak azt, hogy az egyik), akkor a C biztos igaz.
Abszolútérték
Példa (Háromszög egyenlőtlenség) Minden valós x, y számra:
és egyenlőség pontosan akkor áll fenn, ha x, y azonos előjelű.
Mo. Az abszolútérték definíciója: |x|=x, ha x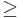 0, és |x|=-x, ha x<0. Esetszétválasztással bizonyítunk. Triviális eset: x=y, akkor |2x|=2|x|=|x|+|x|. Lényeges eset: x≠y. Ekkor az általánosság megszorítása nélkül feltehető, hogy x<y, mert az egyenlőtlenség az x és y felcserélésére nézve szimmetrikus. Ekkor két eset lehetséges:
0, és |x|=-x, ha x<0. Esetszétválasztással bizonyítunk. Triviális eset: x=y, akkor |2x|=2|x|=|x|+|x|. Lényeges eset: x≠y. Ekkor az általánosság megszorítása nélkül feltehető, hogy x<y, mert az egyenlőtlenség az x és y felcserélésére nézve szimmetrikus. Ekkor két eset lehetséges:
1) x, y előjele azonos: ekkor vagy |x|+|y|=x+y=|x+y| vagy |x|+|y|=-x-y=|x+y|,
2) x, y előjele kölönböző. Ekkor |x|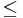 |y| és ekkor |y+x|<|y|
|y| és ekkor |y+x|<|y|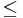 |x|+|y| vagy ellenkezőleg és akkor |x+y|<|x|
|x|+|y| vagy ellenkezőleg és akkor |x+y|<|x|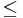 |x|+|y|.
|x|+|y|.
A utolsó esetben egyenlőtlenség növelésére, csökkentésére láttunk példát. Fontos jellemzése az abszolútértékes egyelőltelnségnek a következő: |a|<r, akkor és csak akkor, ha -r<a<+r. Ennek segítségével beláthatjuk, hogy
1. Feladat. Minden valós x, y számra:
és egyenlőség pontosan akkor áll fenn, ha x, y előjele azonos.
Mo. Az előzőek szerint azt kell belátjunk, hogy
Valóban. Minden x-re:
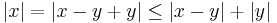 és emiatt:
és emiatt:
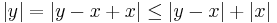
azaz
amely kettő egyszerre pont a keresett egyenlőtlenség.
2. Feladat (Szélsőérték-keresés Descartes módszerével) Igazoljuk, hogy minden x nemnulla valós számra
és egyenlőség pontosan akkor áll fenn, ha |x|=1.
Mo. Mivel az
függvény páros (grafikonja szimmetrikus az y tengelyre) ezért elegendő belátni pozitívokra. Keressük meg azt a pontot, ahol a f(x) és a c konstans egyetlen pontban metszi egymást! Ez pontosan akkor van, ha az f(x)=c egyenletnek két egybeeső gyöke van:
Megj.: f páros, ha minden x∈Dom(f)-re -x∈Dom(f) és f(x)=f(-x).
Indirekt bizonyítás
A tagadás (negáció) kiküszöbölési szabálya az úgy nevezett kettős tagadás törlésének szabálya:
A bevezetési szabálya pedig az úgy nevezett redukció ad abszurdum.
Példa. Igazoljuk, hogy a valós számok halmaza nem sorolható fel egyetlen végtelen sorozatban.
Mo. Indirekten bizonyítunk, a nevezetes Cantor-féle átlós eljárást fogjuk használni. Nos, az biztos, hogy növekvő sorrendbe nem tudjuk felsorolni :) Tekintsük a [0,1] intervallumot és a valós számok tizedestört alakjait. Tegyük fel, hogy van és vegyünk egy tetszőleges felsorolást, (xk)-t:
- x1 = 0, 5 1 0 5 1 1 0 …
- x2 = 0, 4 2 3 2 0 4 3 …
- x3 = 0, 8 2 4 5 0 2 6 …
- x4 = 0, 2 3 3 0 1 2 6 …
- x5 = 0, 4 1 0 7 2 4 6 …
- x6 = 0, 9 9 3 7 8 3 8 …
- x7 = 0, 0 1 0 5 1 3 5 …
- …
Tekintsük a k-adik valós szám k-adik tizedesjegyét, jelöljük ezt xkk-val!
- x1 = 0, 5 1 0 5 1 1 0 …
- x2 = 0, 4 2 3 2 0 4 3 …
- x3 = 0, 8 2 4 5 0 2 6 …
- x4 = 0, 2 3 3 0 1 2 6 …
- x5 = 0, 4 1 0 7 2 4 6 …
- x6 = 0, 9 9 3 7 8 3 8 …
- x7 = 0, 0 1 0 5 1 3 5 …
- …
Most konstruálunk egy tizedestört előállítást. az r szám k-adik jegye legyen 2, ha xkk nem 2 és legyen 0, ha xkk=2. A fenti sorozattal például r=0,2022022... Világos, hogy r valós számot ír le. Most belátjuk, hogy r nem szerepelhet a listában. Tegyük ugyanis fel, hogy valamely m-re xm=r. Ekkor, ha xmm=2, akkor r definíciója miatt xmm=0. De ha xmm nem 2, akkor xmm=2, ami ellentmondás. Tehát az a feltételezésünk, hogy a valósok felsorolhatók ellentmondásra vezet.
Teljes indukció
A teljes indukció olyan következtetési szabály mely csak matematikai környezetben érvényes.
- Kezdő lépés – igazoljuk, hogy 0-ra teljesül A, azaz az aritmetikában bizonyítható A(0)
- Indukciós lépés – feltesszük, hogy egy tetszőleges n természetes számra igaz és bebizonyítjuk, hogy ezesetben a rákövetkezőjére, azaz n + 1-re is igaz lesz A. Tehát belátjuk, hogy az aritmetikában tétel a (∀n)(A(n) ⇒ A(n+1)) kijelentés.
Példa. Igazoljuk, hogy az első n természetes szám összege n(n+1)/2.
Ehhez egy olyan formális leírási módot választunk, ami gyakran előfordul sorozatoknál. Ez az összegzés:
Mo. A kezdő elemre: 1=1, teljesül. Tegyük föl, hogy igaz az n számra. Tudjuk tehát:
Kell:
3. Feladat. Igazoljuk, hogy minden n természetes számra: n<2n.
Mo. n=1-re teljesül. Tegyük fel, hogy valamely n-re n<2n. Kell, hogy
most szorozzuk be az indukciós feltételt 2-vel:
Ezt fogjuk felhasználni:
4. Feladat (Az összegzés tulajdonságai)
Mo. 3-as: n=1-re teljesül. Indukciós eset. Kell: