OptMod-2017/Gyakorlat1

Ismétlés

LP feladat általános modellje

Korlátozó feltételek felírjuk a következõ alakban:

$\begin{align} a_{11}x_1 + a_{12}x_2 + \ldots + a_{1n}x_n &\leq b_1\\ a_{21}x_1 + a_{22}x_2 + \ldots + a_{2n}x_n &\leq b_2\\ &\vdots\\ a_{m1}x_1 + a_{m2}x_2 + \ldots + a_{mn}x_n &\leq b_m \end{align}$

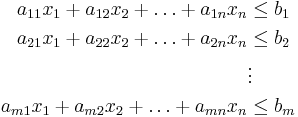
ahol 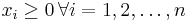$x_i \geq 0 \, \forall i=1,2,\ldots,n$. A célfüggvényt a következõ alakban írjuk fel:

$z = c_1x_1 + c_2x_2 + \ldots + c_nx_n \Rightarrow \text{max vagy min}$

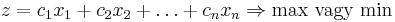
Ugyanez vektorokkal és mátrixokkal:

$\begin{align} \overrightarrow{x} &\geq 0\\ A\overrightarrow{x} &\leq \overrightarrow{b}\\ z=\overrightarrow{c}^T\overrightarrow{x}&\Rightarrow\text{max vagy min} \end{align}$

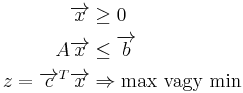
Szimplex módszer

Készítsük el az induló szimplex táblát:

$\begin{array}{c|cccc|c} & x_1 & x_2 & \cdots & x_n & \overrightarrow{b}\\\hline u_1 & a_{11} & a_{12} & \cdots & a_{1n} & b_1\\ u_2 & a_{21} & a_{22} & \cdots & a_{2n} & b_2\\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots\\ u_m & a_{m1} & a_{m2} & \cdots & a_{mn} & b_m\\\hline -z & c_1 & c_2 & \cdots & c_n & 0 \end{array}$

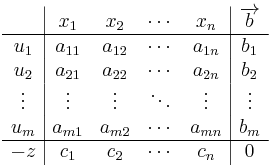
Ha ez megvan, akkor a következõ lépéseket tesszük:

1. Generáló elemet választunk, természetesen csak abból az oszlopból, ahol a célfüggvény együtthatója nem negatív (különben nem növelnénk, hanem csökkentenénk a célfüggvény értékét). Abból az oszlopból érdemes választani, ahol a legnagyobb a célfüggvény együtthatója.
2. Generáló elemnek csak pozitív számot választunk, különben sértenénk a változók nemnegativitását.
3. Azt az elemet választjuk, amelynél a legszûkebb a keresztmetszet, azaz amire 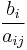$\frac{b_i}{a_{ij}}$ a legkisebb és a_ij pozitív.
4. Ezzel az elemmel pivotálunk (Erre több módszer is van, így mindenki azt használja ami neki kényelmes, csak egyet írok le)
   • A generáló elem oszlopának elemeit osztjuk a generáló elem -1-szeresével.
   • A generáló elem helyére a reciprokát írjuk.
   • A többi elem a szokásos bázistranszformáció és egyenletrendszernél megszokott módszerrel számoljuk.
5. Ha nincs már pozitív célfüggvény együttható, akkor megtaláltuk az optimális megoldást, ha nem tudunk generáló elemet választani, akkor nincs fízibilis megoldása a problémának.

Excel solver

1. feladat

A Kefe Zrt. üzemében 4 féle kefefejet készítenek: K-1, K-2, K-3, és K-4. A kefefejek műanyag sörtékből készülnek, amelyek előállításához különböző minőségű alapanyagokat szoktak beszerezni. Jelenleg az I. osztályúból 22 600 kg, a II. osztályúból 25 400 kg, míg a III. osztályúból 2 600 kg áll rendelkezésre.

A különböző kefefejek természetesen különböző összetételűek. A következő táblázat tartalmazza hogy a különböző kefefejfajták esetén 100 darab elkészítéséhez mennyi és milyen minőségű műanyag szűkséges.

	I.	II.	III.
K-1	9	4	1
K-2	2	7	1
K-3	3	3	0
K-4	0	4	2

Az egyes kefefajták darabjának nyeresége a Kefe Zrt.-nek rendre 30, 22, 13 és 10 Ft.

A) Hány darabot készítsen az üzem a különféle kefefejekből, ha a maximális nyereség elérését tűzték ki célul?

B) Hogyan változik a felírás és a megoldás, ha a választék megtartása érdekében a Kefe Zrt. úgy dönt, hogy a K-1-ból legalább 50 000 db-ot, a K-2-ból legalább 100 000 db-ot, a K-3-ból legalább 300 000 db-ot, a K-4-ból pedig legalább 30 000 db-ot kell az üzemnek gyártania?

2. feladat

Egy vállalat négy fekete teából készíti a Mély Harmónia nevű keverékét. Az alapanyagok: Assam, Darjeeling, Yunan, Ceylon. Három összetevőre kell tekintettel lenni: a frissítő hatást okozó teintartalomra, hogy az se túl sok, se túl kevés ne legyen; a savtartalomra, mert ha az túl sok, akkor nem kellemes a tea íze; és ugyancsak a Mély Harmónia közismerten selymes íze miatt az aromaanyagokra, amelyeknek ismét csak szűk határok között kell lenniük.

Az alábbi táblázat mutatja, hogy a négy eredeti tea idei termése ezekből mennyit tartalmaz, illetve az árukat eurocentben kifejezve, valamint az igényelt alsó és felső korlátot:

tea	tein	sav	aroma	ár
Assam	1,2	4,0	0,4	70
Darjeeling	2	6,5	0,2	44
Yunnan	1,8	5,0	0,25	63
Ceylon	1,6	3,0	0,35	24
alsó korlát	1,59	0	0,3
felsõ korlát	1,61	4,5	0,32

Szeretnénk a lehető legolcsóbb módon a minőségi feltételeknek megfelelő teát előállítani.

3. feladat

A Metro Food Services Company minden reggel friss szendvicsekkel látja el a New York aluljáróiban található automatákat. A cég háromféle szendvicset készít: sajtos-baconos, sonkás, és csirkés.

Egy sajtos-baconos szendvics elkészítése egy munkásnak megközelítőleg 0,45 percbe, egy sonkás szendvics 0,41 percbe, míg egy csirkés szendvics 0,5 percbe telik. A cégnek összesen 16 munkaóra áll rendelkezésére.

Az automaták összkapacitása 2000 szendvics.

A szendvicseken elérhető profit rendre $0,35, $0,42, és $0,37.

Tapasztalatból tudjuk, hogy a vásárlók imádják a bacont, így legalább annyi sajtos-baconos szendvicset fogyasztanak, mint a másik két szendvicsből együttvéve. Ugyanakkor fontos a változatosságnak legalább a látszatát fenntartani, így mindegyik szendvicsből legalább 200-at kell készíteni.

a) Adjunk meg optimális szendvicskészítési stratégiát!

b) A nyereség egy részét vissza szeretnénk forgatni a vállalkozásba. Lehetőségünk van felvenni egy szendvicskészítőt (8 órás munkaidőben), vagy telepíteni egy új, 100 szendvics kapacitású automatát. Melyiket válasszuk?

c) Mennyivel nőne a profitunk, ha nem kötnénk ki, hogy mindegyik szendvicsből kell 200-at készítenünk?

d) Mennyivel nőne a profitunk, ha rosszabb minőségű, de szendvicsenként 5 centtel olcsóbb baconből készítenénk a sajtos-baconös szendvicset? (Próbáljuk meg először újraoptimalizálás nélkül megtippelni az eredményt!)