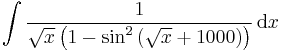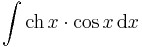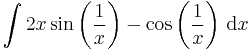Szerkesztő:Mozo/A1 bizonyítások
- Minden tételnek, csak egy bizonyítását kell megtanulni. A benne szereplő fogalmak definícióját ki kell tudni mondani, továbbá példákkal kell tudni illusztrálni, hogy az adott fogalomra van példa illetve ellenpélda. Ha valaki másmilyen bizonyítást szeretne elmondani, annak a következőkhöz kell tartania magát:
- minden felhasznált tételt pontosan ki kell tudni mondani,
- igazolni kell, hogy a felhasznált tétel feltételei az adott szituációban valóban fennállnak,
- pontosan meg kell tudni mondani, hogy a felhasznált tételt az adott körülmények között milyen szereposztásban szándékozunk alkalmazni.
- A QED azt jelenti, hogy ott vége a bizonyításnak.
Tartalomjegyzék |
Bolzano–Weierstrass-tétel
- Ebben a tételben a Bolzano–Weierstrass-tételt fogjuk bizonyítani. Két bizonyítást adunk, de elég csak az egyiket elmondani, azaz vagy a Heine–Boreleset vagy a csúcselemeset. Néhány tételt később a Heine–Borel-tételre fogjuk alapozni.
Heine–Borel-tétellel
Definíció Az U ⊆ R halmaz nyílt, ha minden u ∈ U esetén van olyan ε > 0, hogy az (u-ε , u+ε) nyílt intervallum benne van U-ban.
Definíció Azt mondjuk, hogy a K ⊆ R halmaz kompakt, ha minden olyan esetben, amikor nyílt halmazok uniója lefedi, akkor ezek közül kiválasztható már véges sok nyílt halmaz is, melyeknek uniója még mindig lefedi (röviden: minden nyílt lefedéséből kiválasztható véges részlefedés).
Példa. Az
halmaz kompakt, mert ha lefedi nyílt halmazok egy H halmaza, akkor már a 0-t is lefedi egy U ∈ H nyílt halmaz, azaz van olyan (-ε,+ε) ⊆ U nyílt intervallum, mely lefedi a 0-t. De minthogy (1/n) a 0-hoz konvergál, ezért az (-ε,+ε)-intervallumon kívül csak véges sok tagja van. Emiatt ha veszünk az ezen kívüli véges sok tagot lefedő véges sok H-beli nyílt halmazt és hozzávesszük U-t, akkor ezek már lefedik a halmazt.
Példa. A természetes számok halmaza nem kompakt, mert van olyan nyílt lefedése, melyből biztosan nem választható ki véges részlefedés. Ha ugyanis az n természetes számokat lefedjük az (n-1/2,n+1/2) nyílt intervallumokkal, akkor ennek egyik véges része se fogja az összes természetes számot lefedni.
Tétel – Heine–Borel-tétel – Minden zárt és korlátos intervallum kompakt.
Bizonyítás. A Cantor-féle közösrésztételt fogjuk alkalmazni. Intervallumfelezéses eljárással fogunk definiálni egymásba skatulyázott intervallumok egy sorozatát, melyek hossza a 0-hoz tart.
Legyen az intervallum [a,b]. Legyen egy nyílt lefedése a H halmazrendszer.
Indirekten látjuk be: tegyük fel, hogy [a,b]-nek nincs véges részlefedése. Osszuk [a,b]-t két egyenlő részre, az [a,c] és a [c,b] zárt intervallumokra. Ekkor vagy az [a,b] "baloldali" fele, vagy a "jobboldali" fele olyan, hogy nincs véges részlefedése, ugyanis, ha mindkettőnek lenne, akkor az [a,b]-nek is lenne. Válasszunk ki a két félből most egy olyat, melynek nincs véges részlefedése. Osszuk ezt is két egyenlő részre. Az egyik félnek nincs véges részlefedése, ... folytassuk ezt az eljárást a végtelenségig. Ekkor kapunk egy olyan intervallumsorozatot, melynek következő eleme mindig része a megelőzőnek (In+1 ⊆ In) és a hosszuk a feledés miatt a 0-hoz tart Ekkor a Cantor-tétel miatt létezik a sorozatnak egyetlen közös eleme. Legyen ez u. u-t lefedi egy U ∈ H nyílt halmaz, így egy (u-ε,u+ε) ⊆ U nyílt intervallum is. De mivel az intervallumok hossza a 0-hoz tart, ezért van olyan n, hogy
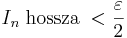 .
.
Ezt viszont benne van (u-ε,u+ε)-ben, mert u benne van In-ben is. Azaz In-nak U véges (egyetlen elemből álló) részlefedése. De ez ellentmondás, mert (In) konstrukciója szerint egyetlen tagjának sincs véges részlefedése. QED
Tétel – Bolzano–Weierstrass-tétel – Minden korlátos sorozatnak van konvergens részsorozata.
Bizonyítás. I. Először belátjuk, hogy a sorozatnak van sűrűsödési pontja. Legyen (an) korlátos sorozat. Ekkor van olyan K szám, hogy minden n-re an ∈ [-K, K]. A [-K, K] korlátos és zárt intervallumra fogjuk alkalmazni a Heine–Borel-tételt. Tegyük fel, hogy (an)-nek nincs sűrűsödési pontja. Ekkor egyik u ∈ [-K, K] sem sűrűsödési pont, azaz az u-hoz található olyan εu > 0 szám, hogy az u körüli 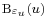 = (u-εu ,u+εu ) intervallumban csak véges sok tagja van a sorozatnak. Az
= (u-εu ,u+εu ) intervallumban csak véges sok tagja van a sorozatnak. Az
halmazrendszer nyílt lefedése [-K, K]-nak, tehát a Heine–Borel-tétel értelmében van véges részlefedése. De, ekkor azt kaptuk, hogy a véges sok olyan halmazzal lehet lefedni a teljes (an)-t, melyekben egyenként is csak véges sok tagja van (an)-nak. Ez ellentmondás, mert ebből az következne, hogy (an)-nek csak véges sok indexe van, ami nem igaz, mert (an) végtelen sorozat.
II. Másodszor kiválasztjuk az így adott sűrűsödési ponthoz konvergáló sorozatot. Legyen δk = 1 / k. Ekkor minden k-ra:
- létezik l > k, hogy
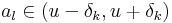
Természetes számok egy nem üres halmazában van legkisebb elem, így legyen minden k-ra
Ekkor az
sorozat az u-hoz tart, mert minden k-ra
QED
Csúcselemmel
- Először belátjuk, hogy minden sorozatból kiválasztható monoton részsorozat, majd belátjuk, hogy monoton-korlátos sorozat konvergens.
Definíció. Azt mondjuk, hogy az (nk) indexsorozat, ha természetes számokból áll és szigorúan monoton növekvő.
Példa. A (pozitív) prímszámok nagyság szerint sorba téve indexsorozatot alkotnak, míg az
sorozat nem.
Definíció. Ha (an) sorozat és (nk) indexsorozat, akkor azt mondjuk, hogy a
összetett függvény az (an) sorozatnak az (nk) indexsorozat által kiválasztott részsorozata.
Tétel – Minden sorozatból kiválasztható monoton részsorozat.
Bizonyítás. Legyen (an) a sorozat. Azt mondjuk, hogy az n-edik tag csúcselem, ha
- minden k > n-ra an > ak.
Esetszétválasztással folytatjuk: vagy véges sok csúcselem van, vagy végtelen sok. Mindkét esetben belátjuk a kívánt sorozat létezését.
1. Tegyük fel, hogy végtelen sok csúcselem van. Ekkor minden k-ra
- létezik l > k, hogy al csúcselem.
Természetes számok egy nemüres halmazában van legkisebb elem, így legyen minden k-ra
Ekkor
monoton csökken, mert vagy következő csúcselem választódik, és akkor csökken, vagy saját maga és akkor nem nő. (Megjegyezzük, hogy ha sorba állítanánk a csúcselemeket indexek szerint, akkor egy szigorúan monoton csökkenő sorozat jönne létre; fent most nem teljesen ezt tettük.)
2. Tegyük fel, hogy véges sok csúcselem van. Ekkor létezik egy legnagyobb indexű 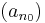 csúcselem. Minden k>0-ra n0 + k már nem csúcselem, így a csúcselem definícióját tagadva:
csúcselem. Minden k>0-ra n0 + k már nem csúcselem, így a csúcselem definícióját tagadva:
- minden k-ra létezik l > n0 + k, hogy
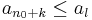 .
.
Rekurzívan definiálunk egy monoton növekvő sorozatot. Legyen
Ha már definiált az nk, akkor tudjuk, ez nem csúcselem, így legyen
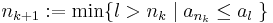 QED.
QED.
Kérdés. Miért kell föltennünk az indexsorozat definíciójában, hogy az szigorúan monoton növekedő sorozat? Ugyanazt a fogalmat kapnánk-e, ha csak azt tennénk fel, hogy 1) monoton nő, 2) végtelenbe tart?
Tétel – Korlátos, monoton sorozat konvergens.
Bizonyítás. Elég belátnunk, hogy korlátos, monoton növekvő (an) sorozat konvergens, mert monoton csökkenő sorozat esetén a (-an) sorozatra alkalmazva ezt az állítást, kapjuk, hogy (an) is konvergens.
Tegyük fel, hogy (an) monoton növekvő sorozat. Ekkor az értékkészlete korlátos, tehát a felsőhatár-axióma miatt van legkisebb felső korlátja:
Definíció szerint belátjuk, hogy a sorozat konvergens és ehhez a számhoz tart. Legyen ε > 0. Ekkor s - ε már nem felső korlát, bár s még az, azaz létezik N, hogy
de mivel a sorozat monoton növekvő, azért minden n > N-re
így minden n > N-re
s mivel ε tetszőleges volt, azért a sorozat konvergál az s-hez. QED
Feladat. Igazolja, hogy ha (an) felülről nem korlátos, akkor van végtelenbe tartó részsorozata! (Pontosan adjon meg egy eljárást, mely egy ilyen részsorozat k-adik tagját produkálja és lássa be róla, hogy valóban végtelenbe tartó sorozatról van szó.)
Feladat. Mi a függvényhatárértékre vonatkozó átviteli elv ("sorozatokkal megfogalmazott vagy Heine-féle függvényhatárérték definíció")? Számítsa ki az alábbi határérték értékét (ha van)! Hol használjuk a számítás közben a L'Hospital szabályt?
Feladat
Heine tétele
Definíció – Egyenletesen folytonosnak mondunk egy f: H  R függvényt a H ⊆ R halmazon, ha:
R függvényt a H ⊆ R halmazon, ha:
Tétel – Heine-tétel – Korlátos és zárt intervallumon értelmezett folytonos függvény egyenletesen folytonos.
Bizonyítás. A Heine–Borel-tételt fogjuk használni. Legyen f: [a,b]  R korlátos és zárt intervallumon értelmezett folytonos függvény. Megadunk [a,b]-nek egy nyílt lefedését. Legyen ε > 0. Ekkor a pontbeli folytonosság definíciója szerint minden egyes u ∈ [a,b] ponthoz létezik olyan δu > 0 pozitív szám, hogy:
R korlátos és zárt intervallumon értelmezett folytonos függvény. Megadunk [a,b]-nek egy nyílt lefedését. Legyen ε > 0. Ekkor a pontbeli folytonosság definíciója szerint minden egyes u ∈ [a,b] ponthoz létezik olyan δu > 0 pozitív szám, hogy:
azaz minden x-re, ha | x - u | < δu akkor | f(x)-f(u) | < ε/2. Legyen tehát :
egy nyílt lefedése [a,b]-nek. A Heine–Borel-tétel szerint létezik véges eleme is, melyek még mindig lefedik [a,b]-t, azaz van V ⊆ [a,b] véges ponthalmaz, hogy
A véges sok δ/2 közül válasszuk a minimálisat:
Minden x,y ∈ H-ra, ha |x-y| < δ, akkor egyfelől az x benne van egy u ∈ V középpontú K-beli intervalumban, másrészt:
Ezért a folytonosság miatt:
QED
Egyenletes folytonosságra bizonyos esetekben következtethetünk nem csak zárt és korlátos esetben is.
Korlátos derivált
Ha az f intervallumon értelmezett differenciálható függvény korlátos deriválttal rendelkezik, akkor a Lagrange-féle középértéktétel miatt f egyenletesen folytonos az értelmezési tartományán. Ugyanis legyen K olyan pozitív szám, hogy minden x ∈ Dom(f)-re:
Ha ε > 0 és δ:=ε/K, akkor minden x,y ∈ Dom(f)-re, ha |x-y| < δ, létezik ξ az x és az y között, hogy azzal:
Példa. Az
egyenletesen folytonos az [1,+∞) halmazon.
Ugyanis, itt korlátos a deriváltja:
Ezért ha x ∈ [1,+∞), akkor
Folytonosan kiterjeszthető függvény
Ha I korlátos, nyílt intervallum és az f I-n folytonos függvénynek létezik véges határértéke az I végpontjaiban, akkor világos, hogy az I lezártja már korlátos és zárt és az f folytonos kiterjesztésére alkalmazható a Heine tétele, amiből következik, hogy f is függvény egyenletesen folytonos (hiszen ugyanaz a delta jó lesz az f-hez is, mint a kiterjesztéséhez).
Példa. A (0,1)-en értelmezett
egyenletesen folytonos a (0,1) intervallumon.
Ugyanis, f folytonosan kiterjed a [0,1] zártra.
Ennél a példánál a korlátos deriváltra nem is hivatkozhattunk volna, mert
nem is korlátos (0,1)-en.
Megjegyezzük, hogy ez az állítás akkor is érvényben marad, ha azt tesszük fel, hogy I akármilyen intervallum, f folytonos és az értelmezési tartománya határpontjaiban létezik és véges a határértéke.
Továbbá bizonyos értelemben ennek az állításnak a megfordítása is igaz. Ha f egyenletesen folytonos, akkor folytonosan (sőt egyenletesen folytonosan) kiterjeszthető az I lezártjára.
Feladat. Igazolja, hogy az ![f(x)=\sin(\sqrt[3]{x})](/upload/math/7/b/2/7b2ed63eaa65f9ac65e2f09a33067941.png) függvény egyenletesen folytonos a teljes R-en! (korlátos derivált és Heine) Deriválható-e f a nullában? (nem)
függvény egyenletesen folytonos a teljes R-en! (korlátos derivált és Heine) Deriválható-e f a nullában? (nem)
Bolzano-tétel
Tétel – Bolzano-tétel – Intervallumon értelmezett, negatív és pozitív értékeket is felvevő folytonos függvénynek van zérushelye.
Bizonyítás. (Cantor-axiómával) https://hu.wikipedia.org/wiki/Bolzano-t%C3%A9tel
(Felső határ axiómával) A Heine-tételt alkalmazzuk. Az általánosság megszorítása nélkül feltehető, hogy a tételbeli f folytonos függvény egy [a,b] intervallum a pontjában negatív, a b pontjában pozitív. (Ellenkező esetben alkalmazzuk a -f függvényre.)
Először is rámutatunk a majdani zérushelyre (majd belátjuk, hogy ez valóban zérushely). f(a) negatív, ezért vegyük a legtávolabbi lehetséges határát annak a halmaznak, ahol f negatív lehet:
(éppenséggel vehettük volna a legkorábbi pontot ahol f már pozitív lehet, az inf{ x ∈ [a,b] | f(x)>0 }), hiszen reménykedünk abban, hogy egy utolsó negatív tartomány után a függvény a folytonosság miatt "felbukkan" és átmetszi az x tengelyt. Belátjuk, hogy minden pozitív ε számra |f(x0)-0| < ε, ami miatt ekkor f(x0)=0 lesz.
Legyen ε > 0 és legyen δ az a pozitív szám, melyet az ε/2 számhoz ad a Heine-tétel (illetve f egyenletes folytonossága). Vegyük [a,b]-nek egy δ-nál kisebb finomságú felosztását (mint az integrálnál). x0 a felosztás egy [c,d] intervallumában van, és feltehető, hogy a belsejében, mert ellenkező esetben finomíthatunk úgy a felosztáson, hogy mégis így álljon a helyzet.
Ekkor egyrészt
mert ha f(d) < 0 lenne, akkor x0 nem lenne a H = { x ∈ [a,b] | f(x)<0 } halmaz felső határa.
Másrészt biztos van a (c,x0] intervallumban olyan e szám, melyre f(e)< 0, mert x0 minden baloldali környezetében van H-beli elem.
Tehát felírhatjuk:
s mivel
ezért
vagyis ezt felhasználva:
QED
Feladat. Igazoljuk, hogy ha f az I intervallumon értelmezett folytonos függvény, és
véges sok szám az intervallumból, akkor létezik olyan ξ ∈ [a1,an], hogy
Használjuk fel, hogy a Bolzano-tételt még olymódon is szokás kimondani, hogy
- intervallumon értelmezett folytonos függvény két függvényértéke között minden értéket fölvesz
melyet Darboux-tulajdonságnak neveznek. A Bolzano-tétel lényegében azt mondja ki, hogy az intervallumon folytonos függvények Darboux-tulajdonságúak. Megjegyezzük, hogy a Darboux-tétel pedig azt mondja ki, hogy az intervallumon differenciálható függvények deriváltfüggvénye Darboux-tulajdonságú.
Feladat. Igazoljuk, hogy ha f: [a,b]  [a,b] folytonos függvény, akkor létezik olyan ξ ∈ [a,b] pont, hogy
[a,b] folytonos függvény, akkor létezik olyan ξ ∈ [a,b] pont, hogy
(az ilyen pontot az f fixpontjának nevezzük).
Feladat. Igazoljuk, hogy az f(x) = x3 + x − sinx függvénynek pontosan egy zérushelye van! Pozitív-e mindenhol a deriváltja? Szigorúan monoton növekvő-e?
Weierstrass tétele
Tétel – Weierstrass-féle minimum-maximum-elv – Korlátos és zárt intervallumon értelmezett folytonos függvény felveszi abszolút minimumát és maximumát.
Bizonyítás. A bizonyítás két részből fog állni. Először belátjuk, hogy minden ilyen függvény korlátos, majd belátjuk, hogy ekkor a maximum és minimum felvétetik.
I. Legyen f:[a,b]  R folytonos. A Heine tétele miatt az ε:=1-hez létezik olyan δ az egyenletes folytonosság definíciójában rögzített megfelelő tulajdonsággal. legyen δ' egy kicsit kisebb, mint δ (mondjuk legyen δ' ∈ (0,δ) rögzített). Vegyük az [a,b] egy δ' finomságú intervallum-felosztását (mint az integrálnál). Ekkor minden ilyen In részintervallumra igaz, hogy például ha an az intervallum bal végpontja, akkor
R folytonos. A Heine tétele miatt az ε:=1-hez létezik olyan δ az egyenletes folytonosság definíciójában rögzített megfelelő tulajdonsággal. legyen δ' egy kicsit kisebb, mint δ (mondjuk legyen δ' ∈ (0,δ) rögzített). Vegyük az [a,b] egy δ' finomságú intervallum-felosztását (mint az integrálnál). Ekkor minden ilyen In részintervallumra igaz, hogy például ha an az intervallum bal végpontja, akkor
azaz az intervallum képe az f(an) ε sugarú környezetébe esik. Tehát a függvény értékkészlete lefedhető véges sok egységsugarú intervallummal. Ez viszont azt jelenti, hogy a függvény korlátos, mert alsó korlátja lesz a legalsó lefedő intervallum alsó végpontja, és felső korlátja a legfelső lefedő intervallum felső végpontja.
II. Belátjuk, hogy f felveszi maximumát (a minimum felvételét ebből úgy látjuk be hogy a most igazolandó tételt alkalmazzuk a -f függvényre). Indirekt módon tegyük fel, hogy f nem veszi fel maximumát, ennek ellenére a korlátossága miatt a
véges. Azaz tulajdonképpen azt tesszük fel, hogy
Definiálunk egy [a,b]-n folytonos függvényt.
A függvény valóban [a,b]-n értelmezett, hiszen a nevező az indirekt feltevés miatt sehol sem lesz nulla. Ezen kívül g folytonos, mert folytonos függvényekből a folytonosságot megőrző módon lett összetéve. Tehát I. miatt korlátos. De a f a sup-hoz végtelen közel kerül, azaz ebből ellentmondást csiholhatunk.
Valóban, közelítsük az S-et a egy függvényérték sorozattal. Ilyen sorozat van, mert ellenkező esetben S nem lenne f felső határa (csak korlátja). Van tehát olyan nem feltétlenül konvergens (xn) sorozat, mely elemei függvényértékeinek sorozata az S-hez tart:
Ekkor
mégpedig a pozitívak felől és éppen ezért
ami ellentmond annak, hogy g korlátos. QED
Feladat. Igazoljuk, hogy ha f: R  R folytonos és létezik a két végtelenben a határértéke és
R folytonos és létezik a két végtelenben a határértéke és
akkor f felveszi abszolút minimumát.
A derivált szakadásai, Darboux-tétel
Intervallumon deriválható függvény deriváltjának nem lehet megszüntethető szakadása. (Ellenben lehet korlátos másodfajú és a végtelen másodfajú szakadása.)
Állítás. Ha f:[a,b]  R folytonos a-ban, differenciálható a nyílton és létezik a derivált határértéke a-ban és ez véges szám, akkor f-nek létezik a deriváltja a-ban (és a deriváltja a lima f' szám).
R folytonos a-ban, differenciálható a nyílton és létezik a derivált határértéke a-ban és ez véges szám, akkor f-nek létezik a deriváltja a-ban (és a deriváltja a lima f' szám).
Bizonyítás. Ez az erős L'Hospital-tétel következménye. Tekintsük a különbségi hányados függvényt, legyen a L'H-beli számláló az x  f(x)-f(a), a nevező az x
f(x)-f(a), a nevező az x  x-a. Világos, hogy a-ban 0/0 alakú, így alkalmazható a L'H-szabály. Ekkor
x-a. Világos, hogy a-ban 0/0 alakú, így alkalmazható a L'H-szabály. Ekkor
azaz létezik a pontbeli derivált és ez a derivált határértéke. QED
Kérdés: hol használtuk fel, hogy az f függvény folytonos?
A deriváltfüggvénynek nem lehet ugrása sem:
Tétel – Darboux-tétel – Ha f:I  R differenciálható, akkor f' Darboux-tulajdonságú (két deriváltérték között a deriváltfüggvény minden értéket fölvesz).
R differenciálható, akkor f' Darboux-tulajdonságú (két deriváltérték között a deriváltfüggvény minden értéket fölvesz).
Bizonyítás. Legyen [a,b] ⊆ I. Az általánosság megszorítása nélkül feltehetjük, hogy f'(a) < f'(b) és f'(a) < m < f'(b) valamely tetszőlegesen rögzített m-re (f'(b) < f'(a) esetén ugyanis a (-f) függvényre teljesülni fog (-f)'(a) < (-f)'(b) és ebből már következik f-re is a tétel). Belátjuk, hogy van olyan ξ ∈ (a,b), hogy f'(ξ) = m. Transzformáljuk el a függvényt, vonjuk ki belőle az x  mx lineárist:
mx lineárist:
g differenciálható, és g'(x) = f'(x) − m, tehát g olyan, hogy tetszőleges x-re:
A feladat tehát, hogy keressünk zérushelyet g'-nek. Ehhez elég, ha találunk g értelmezési tartományának belsejében szélsőértéket, mert akkor a Fermat-féle szélsőértéktétel miatt ott a derivált nulla lesz. [A Fermat-féle szélsőérték tétel azt mondja ki, hogy ha egy függvénynek az értelmezési tartománya egy belső pontjában szélsőértéke van és ott deriválható, akkor a függvény deriváltja ott nulla.] Az [a,b] zárton a folytonos g a Weierstrass-tétel miatt felveszi a szélsőértékeit. Tehát készen vagyunk, amennyiben létezik szélsőérték az (a,b) nyílton. A továbbiakban ezt bizonyítjuk.
Vizsgáljuk a g-t az a-ban. Mivel a feltevés szerint f'(a)<m, ezért f'(a)-m<0 és
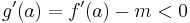 ,
,
ezért
Ekkor természetesen egy valamely ε>0-ra minden x ∈ (a,a+ε)-re
és innen
vagyis a-ban nem lehet g-nek minimuma.
Ha g(b)-t nézzük, akkor m<f'(b), ezért 0<f'(b)-m és
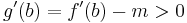 ,
,
ezért valamely ε>0 számmal ha x ∈ (b-ε,b), akkor x-b < 0 és
azaz b-ben sem lehet minimum. Viszont ez azt jelenti, hogy a Weierstrass-tétel által garantált minimum csak az (a,b) nyíltban lehet. QED
Feladat. Adjunk példát olyan deriválható függvényre, melynek a deriváltja egy pontban korlátos módon és olyanra, mely nem korlátos módon szakad.
Feladat. Igazoljuk, hogy ha egy intervallumon differenciálható függvény deriváltja sehol sem nulla, akkor a függvény szigorúan monoton.
Feladat. Igazoljuk, hogy ha 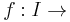 R folytonosan differenciálható és deriváltja sehol sem nulla, akkor invertálható és inverzének deriváltja
R folytonosan differenciálható és deriváltja sehol sem nulla, akkor invertálható és inverzének deriváltja
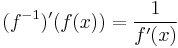 , ha
, ha 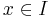 .
.
Feladat. Adjuk meg az f(x) = sin(x) függvényre az
- (f − 1)'(f(x))
kifejezést és ebből a y=f(x) helyen az inverz deriváltját!
Lagrange-tétel
Tétel Lagrange-féle középértéktétel Legyen f: [a,b]  R differenciálható függvény. Ekkor létezik olyan ξ ∈ (a,b), hogy
R differenciálható függvény. Ekkor létezik olyan ξ ∈ (a,b), hogy
Ugyanis, Legyen
Olyan g differenciálható függvény adunk meg, melynek pontosan olyan x helyen van nulla deriváltja, ahol f'(x)=m. Transzformáljuk el az f függvényt az l(x)=m(x-a) függvénnyel:
Ez a függvény egyrészt differenciálható, mert differenciálhatókból van összetéve az azt megőrző módon (speciel, ekkor folytonos is). Másrészt: g(a)=f(a)=g(b). Harmadrészt tetszőleges x ∈ [a,b]-re
A továbbiakban belátjuk, hogy g-nek van az (a,b) nyílton szélsőértéke.
g a Weierstrass-tétel miatt felveszi mindkét típusú extrémumát. Innen esetszétválasztással megyünk tovább.
1) Ha max(g)=f(a) és min(g)=f(a), akkor a függvény konstans, így minden pontja szélsőérték.
2) Ha max(g) és min(g) közül bármelyik nem f(a), akkor ez a valamelyik nem lehet sem a-ban, sem b-ben, mert ott a függvényérték f(a), belül kell, hogy legyen ez a szélsőérték.
Tehát az (a,b)-ben van szélsőértékhely, mondjuk ξ, amire a Fermat-féle szélsőértéktételt alkalmazva kapjuk, hogy
tehát
QED
Feladat. Igazoljuk, hogy intervallumon differenciálható függvény pontosan akkor monoton, ha a deriváltja mindenhol vagy nemnegatív, vagy nempozitív.
Newton–Leibniz-tétel
- A fogalmakra és konkrét példákra vonatkozóan lásd még az utolsó előtti gyakorlat wiki-lapját.
A tételt az analízis második alaptételének is nevezik. Ehhez persze két jelentős fogalmat kell felelevenítenünk. Az egyik a primitív függvény, a másik a Riemann-integrálhatóság fogalma.
Egy [a,b] korlátos és zárt intervallum Riemann-felosztásának nevezzük az olyan függvényt, mely az [a,b] egy véges intervallumokra történő felosztásán van értelmezve és minden intervallumhoz egy benne lévő számot rendel. Tehát, ha
számok, akkor egy Riemann-felbontás az
függvény. Ez δ>0 finomságú, ha a leghosszabb intervalluma is rövidebb mint δ. Az [a,b] intervallum δ finomságú Reimann-felosztásainak halmazát RF[δ[a,b] jelöli.
Az f:[a,b]  R függvény egy η felbontásához tartozó Riemann-közelítő összege a
R függvény egy η felbontásához tartozó Riemann-közelítő összege a
Definíció. Azt mondjuk, hogy a korlátos és zárt intervallumon értelmezett f:[a,b]  R függvény Riemann-integrálható és integrálja az A valós szám, ha
R függvény Riemann-integrálható és integrálja az A valós szám, ha
- minden ε>0-hoz létezik δ>0, hogy minden η∈RFδ[a,b]-re:
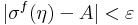
A Riemann-integrálható függvények halmazát az adott intervallumon R[a,b] jelöli.
A másik a primitív függvény fogalma:
Definíció. Azt mondjuk, hogy az F:[a,b]  R differenciálható függvény primitív függvénye az f:[a,b]
R differenciálható függvény primitív függvénye az f:[a,b]  R függvénynek, ha
R függvénynek, ha
- F' = f
Newton–Leibniz-tétel. Legyen f ∈ R[a,b] és létezzen f-nek primitív függvénye éspedig az F. Ekkor
Bizonyítás. Elegendő belátni, hogy ha A-val jelöljük az integrál értékét, akkor A minden számnál közelebb van az F(b)-F(a) értékhez. Legyen ε>0. Az integrálhatóság definíciójából tudjuk, hogy az ε számhoz létezik olyan δ>0, hogy minden η∈RFδ[a,b] felosztásra teljesül, hogy
Tekintsünk egy δ-nál finomabb intervallumfelbontást:
- {[a,x1],...,[xn − 1,b]}
függvényt! Ekkor a részintervallumokra felírható a Lagrange-tétel és minden részintervallumra létezik olyan
szám, hogy az alábbi teleszkopikus összeg előáll integrálközelítő összeg alakjában:
De az
függvény egy δ-nál finomabb Riemann-közelítőösszeg (hiszen a intervallumokat δ-nál rövidebbre választottuk), így ennek eltérése az integráltól kisebb mint ε:
azaz igazoltuk a N–L-formulát.
Feladat Igazoljuk a definíció alapján, hogy az f:[0,1] R, f(0)=0, f(x)=1/x, ha x
R, f(0)=0, f(x)=1/x, ha x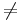 0 függvény és a Dirichlet-függvény (Dir:[0,1]
0 függvény és a Dirichlet-függvény (Dir:[0,1] R; 1, ha x racionális, 0, ha x irracionális)nem Riemann-integrálható.
R; 1, ha x racionális, 0, ha x irracionális)nem Riemann-integrálható.
Feladat R[a,b] az [a,b]-n Riemann-integrálható függvények halmaza, B[a,b] az [a,b]-n korlátos függvények halmaza, M[a,b] az [a,b]-n monoton függvények halmaza, C[a,b] az [a,b]-n a folytonos függvények halmaza. Tudjuk, hogy
- a) C[a,b]⊆R[a,b]
- b) M[a,b]⊆R[a,b] (mert monoton függvénynek csak megszámlálható sok szakadása van és megszámlálható halmaz nullmértékű)
- c) R[a,b]⊆B[a,b].
Igazoljuk, hogy ezek a tartalmazások fordítva nem működnek, azaz mondjuk mindegyik megfordítására ellenpéldát!
Feladat Végezzük el az integrálokat!
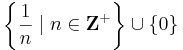
![\{\mathrm{B}_{\varepsilon_{u}}(u)\mid u\in [-K,+K]\}\,](/upload/math/a/0/d/a0df851ee63ac0458a944cb0ce319b68.png)
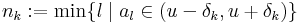
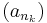
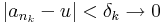
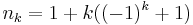
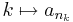
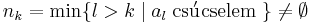
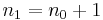
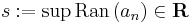
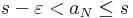
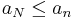
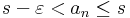
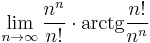
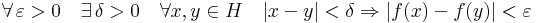
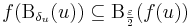
![H=\{\mathrm{B}_{\frac{\delta_u}{2}}(u)\mid u\in [a,b]\}\,](/upload/math/f/4/1/f4108db6735118b5d93f85b4d5e1feee.png)
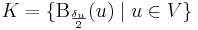
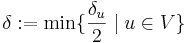
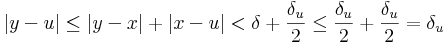
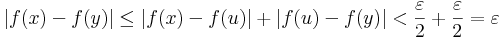
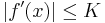
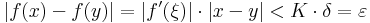
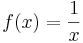
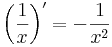
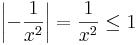
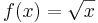
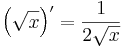
![x_0=\sup\{x\in [a,b]\mid f(x)<0\}](/upload/math/5/6/9/56993663c55e5c9a65b5f66e42994bb5.png)
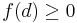
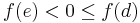
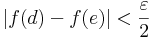
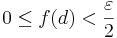
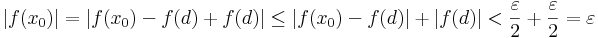
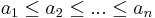
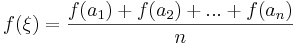
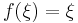
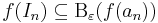
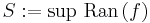
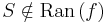
![g(x)=\frac{1}{S-f(x)}\quad\quad(x\in[a,b])](/upload/math/6/8/2/68224515565a21b3f0e0eb4d4c638b56.png)
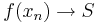
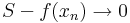
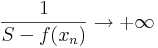
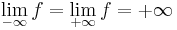
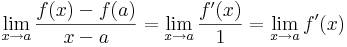
![g(x):=f(x)-mx,\quad\quad x\in[a,b]](/upload/math/6/a/a/6aa43cd2fc4c4d458b4c65f5ec657da4.png)
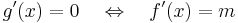
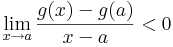
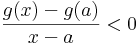
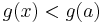
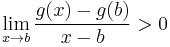
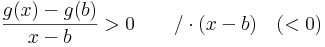
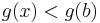
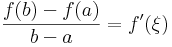
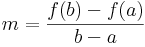
![g(x)=f(x)-m(x-a)\quad\quad(x\in[a,b])](/upload/math/a/3/d/a3d5ab301546f14f71ab5d2316029b1c.png)
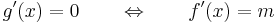
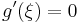
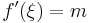
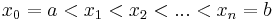
![\eta:\{[a,x_1],...[x_{n-1},b]\}\to [a,b],\quad \eta([x_i,x_{i+1}])\in [x_i,x_{i+1}]](/upload/math/1/3/9/139dc06d9250105c25b8da14886db742.png)
![\sigma^{f}(\eta)=\sum\limits_{i=1}^{n}f(\eta([x_{i-1},x_{i}]))\cdot (x_{i}-x_{i-1})](/upload/math/3/c/8/3c8033aa551c824e2f47b02b7ac9bf6a.png)
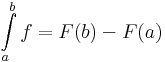
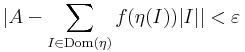
![\eta([x_{i-1},x_i])\in [x_{i-1},x_i]](/upload/math/0/2/a/02a79f3cd70ceb866a394b73c2c69bd2.png)
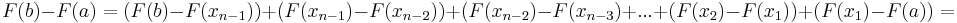
![=F'(\eta([x_{n-1},x_n]))(x_{n}-x_{n-1})+...+F'(\eta([x_{1},x_0])(x_1-x_0)=\sum\limits_{i=1}^nf(\eta([x_{i-1},x_i])(x_{i}-x_{i-1})](/upload/math/e/d/2/ed2980451ccddf5c934eb7782bf65cc6.png)
![[x_{i-1},x_i]\mapsto \eta([x_{i-1},x_i])](/upload/math/e/3/9/e39c49824d0503f8089d513573129a93.png)
![|A-(F(b)-F(a))|=|A-\sum\limits_{i=1}^nf(\eta([x_{i-1},x_i])(x_{i}-x_{i-1})|<\varepsilon](/upload/math/5/4/5/545f3d8b0fdb29a4d4f703ae3e2f40e4.png)