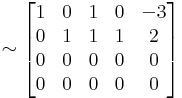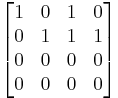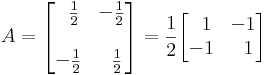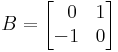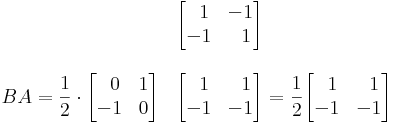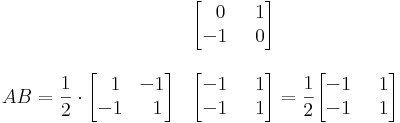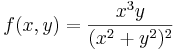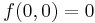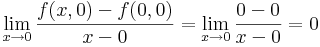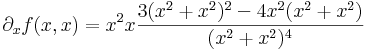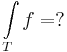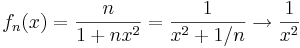Szerkesztő:Mozo/A2 gyakorló feladatok 4
Tartalomjegyzék |
1
Oldja meg az
egyenletrendszert!
Megoldás
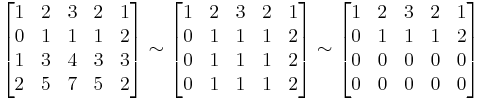
A kibővített mátrix:
Ebből a homogén:
Az Ax = b inhomogén egyenletrendszer megoldása:
- x = xpart + Ker(A)
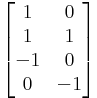
Ehhez dim Ker(A) = 4 - dim Im(A) = 4 - 2 = 2, tehát kétdimenziós a mag: (x=-t+0s, y=-t-s, z=t+0s, w=0t+s vagy (I|B).(B/-I)=B-B=0)
A partikuláris: (-3, 2, 0, 0)
2
Legyen az A operátor R2-ben az y = -x egyenesre vett vetítés, B a 270°-os origó körüli forgatás. Írja fel a leképezések kompozícióinak mátrixát a sztenderd bázisra vonatkozóan. Diagonalizálja ezeket!
Megoldás
Az (1,0) báziselem képe az A által (1/2,-1/2) a (0,1)-é (-1/2,1/2), így:
Valamint
Ekkor
illetve
AB-t nézzük először:

- [AB]2 = T − 1(AB)T
- [BA]2 = T − 1(BA)T
3
Tekintsük az
függvényt, ahol értelmezett, kiterjesztve
-val. Határozzuk meg a parciális deriváltjait (ha vannak) és állapítsa meg, hogy ezek folytonosak-e az origóban!
Megoldás
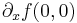 -hez
-hez 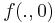 -t kell vizsgálni. A pontbeli parciális derivált a 0-ban:
-t kell vizsgálni. A pontbeli parciális derivált a 0-ban:
ugyanígy az y-szerinti parciális derivált az origóban 0.
Máshol a függvény differenciálhatóakból van összetéve a differenciálhatóságot megőrző módon, így differenciálható. A deriváltfüggvények:
azt látjuk, hogy a számláló 7-odfokú, a nevező 8-ad, így lehet reményünk 1/x-szel az origóban a végtelenhez tartó részsorozat szerkeztésére. Valóban, közelítsük az origót az y = x egyenes mentén. Ekkor a hányados:
ami a 0-ban nem rendelkezik véges határértékkel. ∂xf tehát nem folytonos az origóban.
4
Legyen  ,
,
Legyen f(x,y) = xy6
5
- Konvergens-e?

- Abszolút konvergens-e?
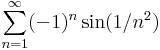
- Egyenletesen konvergens-e?
 ,
, 
Megoldás
6
Find the Fourier series for  on
on ![[0,1]\,](/upload/math/d/0/9/d09694b77d8a3a03f6879fa37f09d0b0.png) .
.
A general formula for the Fourier series of a function on an interval ![[c,c+T]\,](/upload/math/8/3/a/83a43d1a373d5578e7f0fd09507068b1.png) is:
is:
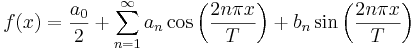
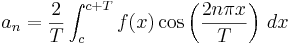

In the current problem,  and
and  .
.

The function  is odd, so the cosine coefficients will all equal zero. Nevertheless,
is odd, so the cosine coefficients will all equal zero. Nevertheless,  should still be calculated separately.
should still be calculated separately.


![= 2\left(\left[\frac{-x \cos 2n\pi x}{2n\pi}\right]_0^1 + \int_0^1 \frac{\cos 2n\pi x}{2n\pi}\,dx\right)\,](/upload/math/2/4/f/24f49401d49eca3e955f5b88959480eb.png)
![= \frac{-1}{n\pi} + \left[\frac{\sin 2n\pi x}{(2n\pi)^2}\right]_0^1 = \frac{-1}{n\pi}\,](/upload/math/8/5/d/85d35d8f8b10bd148cf18f6e37666b79.png)
So the Fourier series for 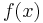 is
is