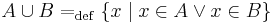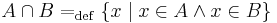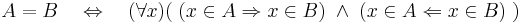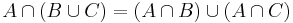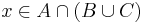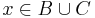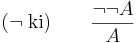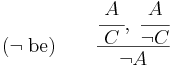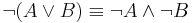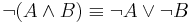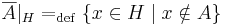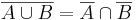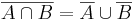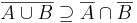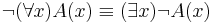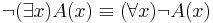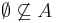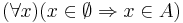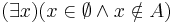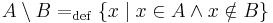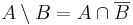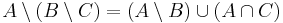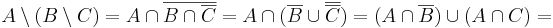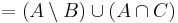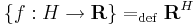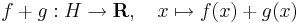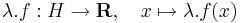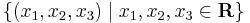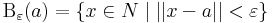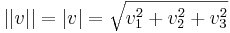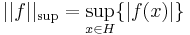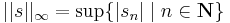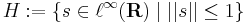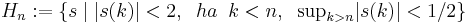Szerkesztő:Mozo/A2 szigorlat 1
Legyenek A és B halmazok. Ekkor A és B uniója:
azaz azon elemek halmaza, mely az A illetve a B közül legalább az egyikben benne vannak;
A és B metszete:
azaz azon elemek halmaza, mely az A-ban is és a B-ben is benne vannak.
Két halmaz egyenlő, akkor és csak akkor, ha ugyanazok az elemeik. Formulákban:
A nyilak a következtetés irányát jelzik.
Igazoljuk a disztributív szabályt (egyik irány)
Bizonyítás. 1) Vegyünk egy tetszőleges x-et. Igazoljuk: "ha x ∈ baloldal, akkor x ∈ jobboldal".
Esetszétválasztás jön, mert innentől nem tudjuk, x a B-ben vagy a C'-ben van
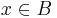
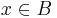 és
és 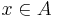 (igaz állítást bármihez "hozzáéselhetünk": és be)
(igaz állítást bármihez "hozzáéselhetünk": és be)
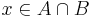
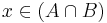 vagy
vagy 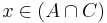 (bármi "hozzávagyolható" egy igaz kijelentéshez: vagy be)
(bármi "hozzávagyolható" egy igaz kijelentéshez: vagy be)
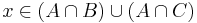
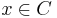
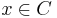 és
és 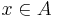 (igaz állítást bármihez "hozzáéselhetünk": és be)
(igaz állítást bármihez "hozzáéselhetünk": és be)
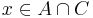
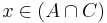 vagy
vagy 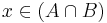 (bármi "hozzávagyolható" egy igaz kijelentéshez: vagy be)
(bármi "hozzávagyolható" egy igaz kijelentéshez: vagy be)
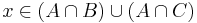
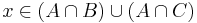 azaz mindkét esetben kijött a jobboldal.
azaz mindkét esetben kijött a jobboldal.
2) Visszafelé ugyanígy, csak felfelé.
A tagadás (negáció) kiküszöbölési szabálya az úgy nevezett kettős tagadás törlésének szabálya:
A bevezetési szabálya pedig az úgy nevezett redukció ad abszurdum.
Ezeknek a segítségével olyan fontos tételeket is levezethetünk, mint a De-Morgan azonosságok:
Ha H halmaz, akkor az A halmaznak a H-ra vonatkozó komplementere az
Ezzel a De-Morgan-azonosságok halmazokkal megfogalmazott változata a következő alakban írható:
A fenti egyenlőségek középiskolából ismert relációval is kifejezhetők. Azt mondjuk, hogy A része B-nek, ha minden olyan esetben, amikor egy elem eleme A-nak, akkor B-nek is eleme, jelben:
Azaz az, hogy A = B az ugyanaz, mint hogy 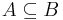 és
és 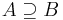 is teljesül.
is teljesül.
esetet.
Vegyünk egy elemet a jobboldalból és igazoljuk, hogy benne van a baloldalban. Tudjuk a metszet definíciója miatt, hogy ekkor
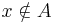
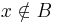
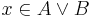 (indirekt feltevés), ezek után esetszétválasztáshoz kell folyamodnunk. Mindkét esetben ellentmondásra jutunk:
(indirekt feltevés), ezek után esetszétválasztáshoz kell folyamodnunk. Mindkét esetben ellentmondásra jutunk:
- ha
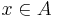 , akkor a legfelső
, akkor a legfelső
- ha
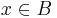 , akkor a legfelső alatti egyenlőség miatt jutunk ellentmondásra, így a
, akkor a legfelső alatti egyenlőség miatt jutunk ellentmondásra, így a
- ha
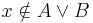 konklúzióra jutottunk.
konklúzióra jutottunk.
Egy másik jellegzetes példa a részhalmaz relációval kapcsolatos. Előtte azonban fel kell idéznünk a kvantorokra vonatkozó De-Morgan-azonosságot. A "létezik" szót (mely a "minden" duálisa) ∃-tel jelöljük:
A kijelentések világosak: ha nem minden dolog A, akkor van olyan dolog, ami nem A. Ha nem létezik A, akkor minden dolog nem A tulajdonságú.
Az üres halmaz minden halmaznak része.
Legyen A tetszőleges halmaz. Indirekten tegyük fel, hogy
Az 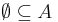 formulákban így néz ki:
formulákban így néz ki:
Egy ilyen tagadása az, hogy a kvantort átírjuk a duálisára és a tulajdonságot tagadjuk:
Ekkor azonban azt kaptuk, hogy létezik az üres halmaznak eleme, ami ellentmondás.
Legyenek A és B halmazok. Ekkor A mínusz B vagy A különbség B:
azaz azon elemek halmaza, melyek az A-nak elemei, de a B-nek nem.
Nagyon hasznos azonosság, hogy a különbség átírható komplementer és metszet segítségével:
ahol a komplementerképzés egy olyan halmazra vonatkoztatjuk, melyben minden szóban forgó halmaz részhalmazként benne van, például jelen esetben H = A U B alkalmas ilyen halmaz .
Tetszőleges A, B és C halmazokra
Írjuk fel a baloldalt és alakítsuk addig, míg ki nem jön a jobboldal:
Legyen H tetszőleges halmaz. Ekkor a
halmazt, azaz a H-n értelmezett R-be képező függvények halmazát függvénytérnek nevezzük. A függvénytér lineáris tér a pontonként műveletekkel, azaz a következőkkel:
ha λ valós szám, akkor
Függvénytér lineáris alterét is függvénytérnek nevezzük. Lineáris altér egy lineáris tér részhalmaza, ha a fenti műveletekre zárt.
Az F függvénytér B részhalmaza bázis, ha B-beli elemek lineáris kombinációjával a tér összes eleme egyértelműen előáll, azaz ha minden f ∈ F-re léteznek egyértelműen olyan λ1, ..., λn számok, hogy
- f = λ1f1 + λ2f2 + ...+ λnfn,
ahol f1, ..., fn ∈ B. B elemszáma a dimenzió.
Példák
1.
 ,
,
melynek elemeit koordinátarendszerben is tudjuk ábrázolni. Természetesen ez végtelen dimenziós.
2. Az intervallumon korlátos függvények B(I) halmaza altere az előzőnek.
3. A zárt és korlátos intervallumon folytonos függvények C[a,b] tere része az a B[a,b]-nek. Ugyanígy a Riemann integrálható függvények is R[a,b] tere is.
4. Legyen H = {1,2,3}. Ekkor az {f:H  R} halmazt még úgy is meg lehet adni, hogy az elemeit egy rendezett hármasba foglaljuk:
R} halmazt még úgy is meg lehet adni, hogy az elemeit egy rendezett hármasba foglaljuk:
Ezt jelöljük R3-nak. R3 minden elemét meg lehet adni 3 előre megadott elem lineráis kombinációjaként: (1,0,0), (0,1,0), (0,0,1). Ezek alkotják R3 sztenderd bázisát (rendes bázis). Általában Rn. Ebbeli függvények analíziséve fogunk foglalkozni.
5. Legyen R2×3 a 2-szer 3-as mátrixok tere. Ez szintén lineáris tér az elemenkénti összeadással és a skalárral szorzással. A bázisa 6 elemű.
6. {s:Z  R} a sorozatok (vagy a polinomok tere). Ez végtelen dimenziós és a báziselemek a hatványfüggvények.
R} a sorozatok (vagy a polinomok tere). Ez végtelen dimenziós és a báziselemek a hatványfüggvények.
Az N vektortéren értelmezett
- ||.||: N
 R
R
függvény norma N-en, ha
- ||v||
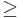 0 minden v ∈ N-re és v=0, ha ||v|| = 0.
0 minden v ∈ N-re és v=0, ha ||v|| = 0.
- minden λ számra és v ∈ N-re |λ|
 ||v||=||λ.v||
||v||=||λ.v||
- ||u + v||
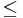 ||u|| + ||v||
||u|| + ||v||
Ekkor N a ||.||-val ellátva normált tér.
ε > 0 sugarú a ∈ N középpontú nyílt gömb:
Példa. A főpéldán, az R3-en, ez az euklideszi vektorhossz, azaz a Pithagorasz-tételből kiszámítható
Példa. Két lényeges Rn-beli norma.
- p>0, akkor
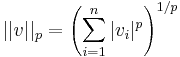
-
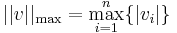
Érdemes megnézni, hogy a gömbök R2-ben hogy néznek ki. ||.||1 esetén a gömb egy csúcsára állított négyzet 2 ε átlóval. ||.||max egy oldalára állított négyzet. ||.||2pedig egy körlap.
Függvénytéren a leggyakoribb norma a szuprémumnorma. Ha B(H,R) a H  R korlátos függvények tere, akkor ennek akármilyen alterén norma az
R korlátos függvények tere, akkor ennek akármilyen alterén norma az
u belső pontja H-nak, ha van olyan (gömbi) környezete u-nak, mely teljes egészében H-beli. H nyílt halmaz, ha minden pontja belső pont. H zárt, ha komplementere, azaz az
halmaz nyílt.
Tétel. Minden véges dimenziós normált tér ekvivalens egymással topologikus szempontból, azaz bármelyik norma ugyanazokat a nyílt halmazokat határozza meg.
Célszerű tehát a feladatokban választani például azt a p-edik normát, mellyel a legkönnyebben lehet számolni.
Világos, hogy Rn nyílt halmaz, így ennek komplementere, az üres halmaz zárt. Ám, az üres halmaz nyílt is, hiszen minden pontja belső pont. Ha ugyanis lenne olyan pontja, ami nem belső pontja, akkor lenne egyáltalán pontja, ami lehetetlen, lévén az üres halmaz üres. Így komplementere, azaz Rn zárt halmaz is. Tanulság: vannak nyílt-zárt halmazok (clopen in English) és vannak se nem nyílt, se nem zárt halmazok, például a [0,1) intervallum. Vagyis "a halmaz nem ajtó, ami vagy nyílt, vagy zárt"!
Véges sok nyílt halmaz metszete nyílt, akármennyi nyílt halmaz uniója nyílt. A zártakra a duális állítás igaz: véges sok zárt halmaz uniója zárt, akárhány zárt halmaz metszete zárt.
- Igazoljuk, hogy végtelen sok nyílt halmaz uniója nyílt!
- Igazoljuk, hogy véges sok nyílt halmaz metszete nyílt!
- Adjuk példát végtelen sok nyílt halmazra, amelyek metszete nem nyílt!
- Adjuk példát végtelen sok zárt halmazra, amelyek uniója nem zárt!
Kompakt egy K halmaz, ha minden nyílt halmazrendszerből, melynek uniója lefedi K-t kiválasztható véges sok nyílt halmaz is, melyek véges uniója még mindig lefedi K-t.
Heine-Borel-tétel. Véges dimenziós normált térben korlátos és zárt halmaz kompakt.
Rn véges dimenziószáma nagyon lényegesen hozzájárul a fenti tételek fennállásához. Általában (Haussdorf-térben) kompakt halmaz korlátos és zárt. Ám, van olyan végtelen dimenziós normált tér, melyben zárt és korlátos halmaz nem kompakt. Legyen ugyanis 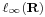 a korlátos sorozatok tere. A téren a norma a suprémum:
a korlátos sorozatok tere. A téren a norma a suprémum:
Példa.
"gömb" zárt, korlátos, de nem kompakt.
Ugyanis, Nyilván korlátos, mert belefoglalható a B2(0) kétség sugarú 0 körüli gömbbe. Zárt is, ehhez nézzük a komplementerét! Ha ||s||> 1, az pontosan azt jelenti, hogy sup s >1, azaz létezik olyan ε>0, hogy minden n-re |s(n)| > 1+ ε. Pozitív s(n)-re vegyük az s(n)>(s(n)+1+ε)/2 > 1+ε, negatív tagokra az s(n)<(s(n)+(-1-epsilon))/2<-1-ε elemekből álló t sorozatot. Ez a komplementerben halad, mert sup |t| > 1+(ε/2).
De nem kompakt. Fedjük le ugyanis a
halmazokkal! Ezek nyíltak, de véges sok nem fedi le H-t.
Hasonló furcsaságok jelentkeznek a p-edik hatványon szummálható sorozatok 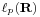 terében is. Számunkra esetleg a véges sorösszeggel rendelkező
terében is. Számunkra esetleg a véges sorösszeggel rendelkező 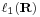 tér bír jelentőséggel.
tér bír jelentőséggel.