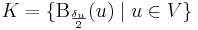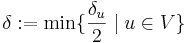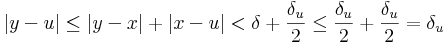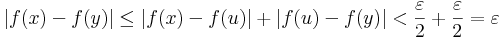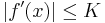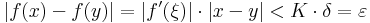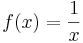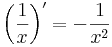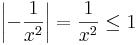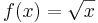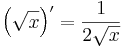Szerkesztő:Mozo/A2 szigorlat 6
Definíció – Egyenletesen folytonosnak mondunk egy f: H  R függvényt a H ⊆ R halmazon, ha:
R függvényt a H ⊆ R halmazon, ha:
Tétel – Heine-tétel – Korlátos és zárt intervallumon értelmezett folytonos függvény egyenletesen folytonos.
Bizonyítás. A Heine–Borel-tételt fogjuk használni. Legyen f: [a,b]  R korlátos és zárt intervallumon értelmezett folytonos függvény. Megadunk [a,b]-nek egy nyílt lefedését. Legyen ε > 0. Ekkor a pontbeli folytonosság definíciója szerint minden egyes u ∈ [a,b] ponthoz létezik olyan δu > 0 pozitív szám, hogy:
R korlátos és zárt intervallumon értelmezett folytonos függvény. Megadunk [a,b]-nek egy nyílt lefedését. Legyen ε > 0. Ekkor a pontbeli folytonosság definíciója szerint minden egyes u ∈ [a,b] ponthoz létezik olyan δu > 0 pozitív szám, hogy:
azaz minden x-re, ha | x - u | < δu akkor | f(x)-f(u) | < ε/2. Legyen tehát :
egy nyílt lefedése [a,b]-nek. A Heine–Borel-tétel szerint létezik véges eleme is, melyek még mindig lefedik [a,b]-t, azaz van V ⊆ [a,b] véges ponthalmaz, hogy
A véges sok δ/2 közül válasszuk a minimálisat:
Minden x,y ∈ H-ra, ha |x-y| < δ, akkor egyfelől az x benne van egy u ∈ V középpontú K-beli intervalumban, másrészt:
Ezért a folytonosság miatt:
QED
Egyenletes folytonosságra bizonyos esetekben következtethetünk nem csak zárt és korlátos esetben is.
Korlátos derivált
Ha az f intervallumon értelmezett differenciálható függvény korlátos deriválttal rendelkezik, akkor a Lagrange-féle középértéktétel miatt f egyenletesen folytonos az értelmezési tartományán. Ugyanis legyen K olyan pozitív szám, hogy minden x ∈ Dom(f)-re:
Ha ε > 0 és δ:=ε/K, akkor minden x,y ∈ Dom(f)-re, ha |x-y| < δ, létezik ξ az x és az y között, hogy azzal:
Példa. Az
egyenletesen folytonos az [1,+∞) halmazon.
Ugyanis, itt korlátos a deriváltja:
Ezért ha x ∈ [1,+∞), akkor
Folytonosan kiterjeszthető függvény
Ha I korlátos, nyílt intervallum és az f I-n folytonos függvénynek létezik véges határértéke az I végpontjaiban, akkor világos, hogy az I lezártja már korlátos és zárt és az f folytonos kiterjesztésére alkalmazható a Heine tétele, amiből következik, hogy f is függvény egyenletesen folytonos (hiszen ugyanaz a delta jó lesz az f-hez is, mint a kiterjesztéséhez).
Példa. A (0,1)-en értelmezett
egyenletesen folytonos a (0,1) intervallumon.
Ugyanis, f folytonosan kiterjed a [0,1] zártra.
Ennél a példánál a korlátos deriváltra nem is hivatkozthattunk volna, mert
nem is korlátos (0,1)-en.
Megjegyezzük, hogy ez az állítás akkor is érvényben marad, ha azt tesszük fel, hogy I akármilyen intervallum, f folytonos és az értelmezési tartománya határpontjaiban létezik és véges a határértéke.
Továbbá bizonyos értelemben ennek az állításnak a megfordítása is igaz. Tétel Ha f egyenletesen folytonos, akkor egyenletesen folytonosan kiterjeszthető az I lezártjára. Ez folytonosságra nem igaz, mondjunk ellenpéldát!
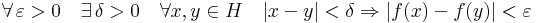
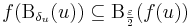
![H=\{\mathrm{B}_{\frac{\delta_u}{2}}(u)\mid u\in [a,b]\}\,](/upload/math/f/4/1/f4108db6735118b5d93f85b4d5e1feee.png)