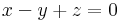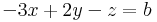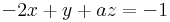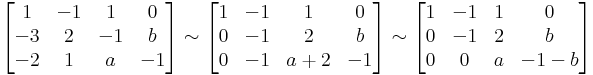Vita:Gauss-elimináció
Ez így kezdetnek jó? Nyariz 2008. február 1., 23:51 (CET)
Nagyon jó! :) Mondjuk ezt a redukált lépcsős alak meg ilyenek, az lehet, hogy első olvasásra ijesztő. Akármilyen furcsának hangzik, a példánál kéne kezdeni és azt mondani, hogy minden olyan művelet elvégezhető, ami az egyenletrendszerek rendezésénél. Aztán utána össze lehet foglalni a fő lépéseket. (Sztem.) Mozo 2008. február 2., 07:15 (CET)
Megoldottam a példát ilyen táblázatos formában, szerintem ez így elég szemléletes. Ha az így jó akkor majd megírom a másikat is. Amúgy a leírás tényleg egy kicsit ijesztő, de ha valaki első olvasásra nem érti, úgyis megnézi a példát az alapján megérti, és utána a leírást is érteni fogja. De nincs akadálya annak, hogy előretegyük a példát, hacsak nem akarunk követni valamiféle "style guidelines"-t.:) Nyariz 2008. február 7., 12:08 (CET)
Szép lett, irigylésre méltó :), a táblázatszerekesztésed kapcsán csak nézek, mint tengerimalac az akváriumban :) !
Azért két dolgot kihangsúlyoznék:
- van egy kevésbé szigorú és algoritmikus módja a Gaussolásnak, amikor igyekszünk mindig egész számokat készíteni a táblázatban, az egyenlő együtthatók megoldási módszeréhez hasonlóan. ez ugyanolyan alkalmas a rang és függetlenségvizsgálatokra. A másik, amit Te is csinálsz, az a szigorú algoritmus, amikor kivonod a 2. sorból az első sor a_21/a_11 szeresét. Ez például az úgy nevezett LU felbontásra is alkalmas, ami fontos numerikus módszer (bár nekünk nem kell)(LU decomposition)
- továbbá élesen válasszuk szét a Gauss és a Gauss-Jordan módszert (ahogy Serény is megkülönbözteti), az utóbbiban a főátlót "leeggyezzük" és továbbcsináljuk a felső háromszög lenullázását.
Az egyenletrendszerek megoldásánál ezeken túl biztos szólni kéne a megoldásszám diszkussziójáról. Gondolj bele milyen elegáns lesz amikor a Serény megkérdezi ZH-ben, hogy "Van-e megoldása és ha igen hány darab az alábbi egyenletrendszernek?" Ekkor biztos nem kell majd végigcsinálni az algoritmust, csak a lépcsős alakig és abból következtetni a válaszra. Mozo 2008. február 7., 14:02 (CET)
- Akkor megoldást írjam át a nem szigorúra? A megoldások számánál meg elég a tilos sorokról meg a szabad paraméterekről beszélni? A gauss-jordanről mit írjak? Annyit, hogy van az is de az nem ez? Nyariz 2008. február 7., 17:06 (CET)
- Nyugi, majd kigondolom. Lehet, hogy egy külön szócikk kéne a lin. egyenletrendszerre? Nem tudom. A nem szigorú az, amikor megengedjük magunknak, hogy egy sort beszorozzunk 3-mal, a másikat meg 4-gyel. A szigorúnál osztani, szorozni nem lehet egy sort, mert akkor a determináns értéke megváltozhat -- persze nemnullából nem lesz nulla determinánsú, így rangon és a megoldhatóságon nem változtat -- csak emberszerűbb lesz. A lényeg, hogy amit írtál az tök jó és most ez a fontos! :) Mozo 2008. február 7., 19:25 (CET)
- Szerintem mindenképp kéne egy külön lineáris egyenletrendszer szócikk hasonlóan az angol wikipediához, és onnan lehetne link a Gauss-eliminációra Cramer-szabályra stb. Nyariz 2008. február 7., 21:00 (CET)
- Nyugi, majd kigondolom. Lehet, hogy egy külön szócikk kéne a lin. egyenletrendszerre? Nem tudom. A nem szigorú az, amikor megengedjük magunknak, hogy egy sort beszorozzunk 3-mal, a másikat meg 4-gyel. A szigorúnál osztani, szorozni nem lehet egy sort, mert akkor a determináns értéke megváltozhat -- persze nemnullából nem lesz nulla determinánsú, így rangon és a megoldhatóságon nem változtat -- csak emberszerűbb lesz. A lényeg, hogy amit írtál az tök jó és most ez a fontos! :) Mozo 2008. február 7., 19:25 (CET)
Még egy apróság: a mátrixot jelölésére melyik jelölést használjuk? mert én itt a bmatrix-ot, mint az angol wikipedian, a mátrix rangja szócikknél pmatrix van de mondjuk könyvekben gyakran látok vmatrix-ot.
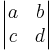 szokásos jelölése a
szokásos jelölése a 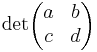 determinánsnak, ezért nem javasolt használni mátrixként.
determinánsnak, ezért nem javasolt használni mátrixként.
A másik kett közül tökmindegy melyiket használod. Én meg aztán pláne nem vagyok következetes, így nálam teljesen keveredik a két jelölés. Az a lényeg, hogy a determinánstól jól elüssön.
A gnuplot kép nagyon szép lett! Mozo 2008. február 8., 21:47 (CET)
Tartalomjegyzék |
Paraméteres egyenletrendszer
1.
megoldható pontosan akkor, ha a-1=0 esetén, b=0 és a-1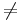 0 esetén b bármilyen. Az első esetben végtelen sok megoldás, a másodikban 1, tehát:
0 esetén b bármilyen. Az első esetben végtelen sok megoldás, a másodikban 1, tehát:
- 0 megoldás, ha (a,b) ∈ {1} × R\{0}, mert ekkor 0x+0y+0z=b
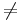 0 ellentomodó egyenlet
0 ellentomodó egyenlet
- 1 megoldás, ha (a,b) ∈ R\{1} × R, mert ekkor det A
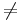 0
0
- ∞ megoldás, ha (a,b)=(1,0), mert ekkor det A = 0 és nem ellentmondó az alsó egyenlet: 0x+0y+0z=0Mozo 2008. március 10., 10:22 (CET)
2.
Diszkusszió:
1) Van megoldás pontosan akkor, ha 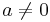 és b bármilyen vagy a = 0 és b = -1 (ekkor az ehómátrix és a kibővített mátrix rangja egyenlő (3 ill. 2).
2) Ha van megoldás, akkor ez előbb említett első esetben 1 db megoldás van, az utóbb említett esetben végtelen sok. Mozo 2008. március 12., 14:57 (CET)
és b bármilyen vagy a = 0 és b = -1 (ekkor az ehómátrix és a kibővített mátrix rangja egyenlő (3 ill. 2).
2) Ha van megoldás, akkor ez előbb említett első esetben 1 db megoldás van, az utóbb említett esetben végtelen sok. Mozo 2008. március 12., 14:57 (CET)
Paraméteres determináns
Milyen c-re nulla az alábbi determináns értéke?
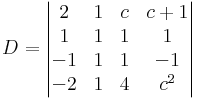 a 2. oszlop csupa 1, és a többiben is van sok egyes, tehát érdemes levonni a 2. oszlopot a többiből:
a 2. oszlop csupa 1, és a többiben is van sok egyes, tehát érdemes levonni a 2. oszlopot a többiből:
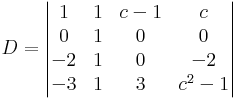 a 2. sorban egy db 1-es lett, fejtsük ki eszerint:
a 2. sorban egy db 1-es lett, fejtsük ki eszerint:
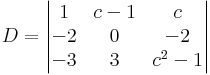 ha levonjuk az 1. oszlopot a 3-ból, akkor eltűnik a -2:
ha levonjuk az 1. oszlopot a 3-ból, akkor eltűnik a -2:
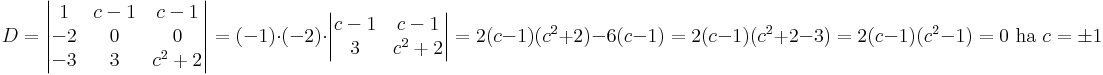
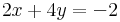
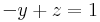
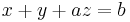
![[\mathbf{A}|\mathbf{y}]\sim\begin{bmatrix}
2 & 4 & 0 & -2\\
0 & -1 & 1 & 1\\
1 & 1 & a & b
\end{bmatrix}\sim\begin{bmatrix}
1 & 2 & 0 & -1\\
0 & -1 & 1 & 1\\
0 & -1 & a & b+1
\end{bmatrix} \sim\begin{bmatrix}
1 & 2 & 0 & -1\\
0 & -1 & 1 & 1\\
0 & 0 & a-1 & b
\end{bmatrix}](/upload/math/c/a/b/cab81a691ddeb6ecca0f1a637a50da1a.png)