Bolzano–Weierstrass-tételkör

A MathWikiből

(Változatok közti eltérés)

A lap 2008. május 20., 22:11-kori változata

A Bolzano--Weierstrass-tétel és a hozzá kapcsolódó állítások Rⁿ jellegzetes topologiai tulajdonságaira mutatnak rá. Lényegében a korlátos és zárt halmazok kompaktságáról szólnak.

Tartalomjegyzék

1 Sorozatkompaktság és B--W-tétel

Sorozatkompaktság és B--W-tétel

Egy K halmaz sorozatkompakt Rⁿ-ben, ha minden benne a K-ban haladó sorozatból kiválasztható K-beli határértékű konvergens részsorozat. Jelekben:

K sorozatkompakt

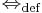
$\Leftrightarrow_{\mathrm{def}}$

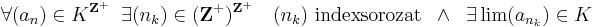
$\forall(a_n)\in K^{\mathbf{Z}^+}\;\;\exists(n_k)\in (\mathbf{Z}^+)^{\mathbf{Z}^+}\quad (n_k)\mbox{ indexsorozat} \;\;\wedge\;\; \exists\lim(a_{n_k})\in K$

A konvergens részsorozatra vonatkozó tétel Rⁿ-ben:

Bolzano-Weierstrass-féle kiválasztási tétel. Korlátos sorozatnak van konvergens részsorozata.

Bizonyítását külön nézzük az egy és a többváltozós esetre.

Az egyváltozós eset

Bizonyítás csúcselemmel

Belátjuk, hogy minden valós sorozatból kiválasztható monoton részsorozat.

Ehhez először vezessük be a csúcselem fogalmát. $a k$ -t csúcselemnek nevezzük, ha minden 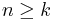$n \geq k$ esetén 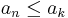$a_n \leq a_k$ . (Vagyis azokat az elemeket nevezzük így, amelyeknél a nagyobb indexű elemek között nincs nagyobb.)

Ekkor két eset lehetséges:

Végtelen sok csúcselem van a sorozatban. Ha 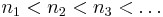$n_1 < n_2 < n_3 < \ldots$ indexek, melyekre 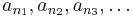$a_{n_1}, a_{n_2}, a_{n_3}, \ldots$ csúcselemek, akkor ez utóbbi sorozat nyilvánvalóan monoton csökkenő.
Véges sok csúcselem van a sorozatban. Vagyis létezik $n 0$ , hogy minden $n > n 0$ esetén $a n$ nem csúcselem.

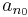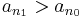De $a_{n_0}$ nem csúcselem, vagyis létezik $n 1 > n 0$ , hogy $a_{n_1} > a_{n_0}$ .
De 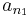$a_{n_1}$ nem csúcselem, vagyis létezik $n 2 > n 1$ , hogy 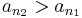$a_{n_2} > a_{n_1}$ stb.

Ekkor viszont 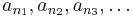$a_{n_1}, a_{n_2}, a_{n_3}, \ldots$ nyilván szigorúan monoton növő sorozat.

Vagyis minden sorozatnak van monoton részsorozata. De a mi sorozatunk egyben korlátos is, márpedig korlátos monoton sorozat konvergens.

Borel–Lebesgue-tétellel

Azt fogjuk belátni, hogy a sorozatnak van sűrűsödési pontja, azaz olyan pont, melynek minden nyílt környezetében van végtelen sok sorozatbeli elem. Ekkor ugyanis már kiválasztható az u sűrűsödési helyhez konvergáló részsorozat: minden n-re: $b n$ = min{ i > n | |a_i-u| < δ $n$ }, ahol δ $n$ egy szigorúan monoton csökkenő nullsorozat.

Legyen $[a, b]$ olyan korlátos és zárt intervallum, mely lefedi a sorozatot. Tegyük fel indirekt módon, hogy $a n$ -nek nincs sűrűsödési helye. Ekkor minden $x$ ∈ $[a, b]$ -nek létezik olyan nyílt környezete, melyben csak véges sok sorozatbeli elem van. Az $[a, b]$ intervallum ezen halmazokból álló nyílt lefedéséből kiválasztható véges sok, mely még mindig lefedés, éspedig a Borel–Lebesgue-tétel miatt. Tehát a sorozatnak összesen véges sok szor véges sok, azaz véges sok eleme eshet $[a, b]$ -be, ami ellentmond annak, hogy a sorozatnak végtelen sok tagja van és ez mind $[a, b]$ -ben van.

Többváltozós eset

Bizonyítás. Direktben a csúcselemes bizonyítás nem működik (nincs rendezés). Komponensenként sem működik! De egymás után komponensről komponensre haladva, egyre szűkebb részsorozatokat kiválasztva már tud működni.

Kompakt egy K halmaz, ha minden nyílt halmazrendszerből, melynek uniója lefedi K-t kiválasztható véges sok nyílt halmaz is, melyek véges uniója még mindig lefedi K-t.

Heine-Borel-tétel. Korlátos és zárt halmaz kompakt.

Rⁿ-ben tehát a kompaktság ugyanaz, mint a sorozatkompaktság.

Rⁿ véges dimenziószáma nagyon lényegesen hozzájárul a fenti tételek fennállásához. Általában (Haussdorf-térben) kompakt halmaz korlátos és zárt. Ám, van olyan végtelen dimenziós normált tér, melyben zárt és korlátos halmaz nem kompakt. Legyen ugyanis 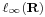$\mbox{ }_{\ell_{\infty}(\mathbf{R})}$ a korlátos sorozatok tere. A téren a norma a suprémum:

$||s||_{\infty}=\sup\{|s_n|\mid n\in\mathbf{N}\}$

Ekkor a

$H:=\{s\in\ell^{\infty}(\mathbf{R})\mid ||s||\leq 1\}$

"gömb" nem kompakt. Hasonló furcsaságokat jelentkeznek a p-edik hatványon szummálható sorozatok 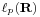$\mbox{ }_{\ell_{p}(\mathbf{R})}$ terében is. Számunkra esetleg a véges sorösszeggel rendelkező 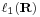$\mbox{ }_{\ell_{1}(\mathbf{R})}$ tér bír jelentőséggel.

@@ 7. sor: / 7. sor: @@
 :<math>\forall(a_n)\in K^{\mathbf{Z}^+}\;\;\exists(n_k)\in (\mathbf{Z}^+)^{\mathbf{Z}^+}\quad (n_k)\mbox{ indexsorozat} \;\;\wedge\;\; \exists\lim(a_{n_k})\in K </math>
-Az egyváltozós esetből adódik a tétel maga:
+A konvergens részsorozatra vonatkozó tétel '''R'''<sup>n</sup>-ben:
 '''Bolzano-Weierstrass-féle kiválasztási tétel.''' Korlátos sorozatnak van konvergens részsorozata.
+Bizonyítását külön nézzük az egy és a többváltozós esetre.
+===Az egyváltozós eset===
+:''Bizonyítás csúcselemmel''
+Belátjuk, hogy minden valós sorozatból kiválasztható [[monoton]] [[részsorozat]].
+Ehhez először vezessük be a ''csúcselem'' fogalmát. <math>a_k</math>-t csúcselemnek nevezzük, ha minden <math>n \geq k</math> esetén <math>a_n \leq a_k</math>. (Vagyis azokat az elemeket nevezzük így, amelyeknél a nagyobb indexű elemek között nincs nagyobb.)
+Ekkor két eset lehetséges:
+# [[Végtelen]] sok csúcselem van a sorozatban. Ha <math>n_1 < n_2 < n_3 < \ldots</math> indexek, melyekre <math>a_{n_1}, a_{n_2}, a_{n_3}, \ldots</math> csúcselemek, akkor ez utóbbi sorozat nyilvánvalóan monoton csökkenő.
+# Véges sok csúcselem van a sorozatban. Vagyis létezik <math>n_0</math>, hogy minden <math>n>n_0</math> esetén <math>a_n</math> nem csúcselem.
+*De <math>a_{n_0}</math> nem csúcselem, vagyis létezik <math>n_1 > n_0</math>, hogy <math>a_{n_1} > a_{n_0}</math>.
+*De <math>a_{n_1}</math> nem csúcselem, vagyis létezik <math>n_2 > n_1</math>, hogy <math>a_{n_2} > a_{n_1}</math> stb.
+Ekkor viszont <math>a_{n_1}, a_{n_2}, a_{n_3}, \ldots</math> nyilván szigorúan monoton növő sorozat.
+Vagyis minden sorozatnak van monoton részsorozata. De a mi sorozatunk egyben korlátos is, márpedig korlátos monoton sorozat konvergens.
+===Borel–Lebesgue-tétellel===
+Azt fogjuk belátni, hogy a sorozatnak van sűrűsödési pontja, azaz olyan pont, melynek minden nyílt környezetében van végtelen sok sorozatbeli elem. Ekkor ugyanis már kiválasztható az ''u'' sűrűsödési helyhez konvergáló részsorozat: minden ''n''-re: <math>b_n</math> = min{ i > n | |a_i-u| < &delta;<math>_n</math>}, ahol &delta;<math>_n</math> egy szigorúan monoton csökkenő nullsorozat.
+Legyen <math>[a,b]</math> olyan korlátos és zárt intervallum, mely lefedi a sorozatot. Tegyük fel indirekt módon, hogy <math>a_n</math>-nek nincs sűrűsödési helye. Ekkor minden <math>x</math> &isin; <math>[a,b]</math>-nek létezik olyan nyílt környezete, melyben csak véges sok sorozatbeli elem van. Az <math>[a,b]</math> intervallum ezen halmazokból álló nyílt lefedéséből kiválasztható véges sok, mely még mindig lefedés, éspedig a [[Borel–Lebesgue-tétel]] miatt. Tehát a sorozatnak összesen véges sok szor véges sok, azaz véges sok eleme eshet <math>[a,b]</math>-be, ami ellentmond annak, hogy a sorozatnak végtelen sok tagja van és ez mind <math>[a,b]</math>-ben van.
+===Többváltozós eset===
 ''Bizonyítás.'' Direktben a csúcselemes bizonyítás nem működik (nincs rendezés). Komponensenként sem működik! De egymás után komponensről komponensre haladva, egyre szűkebb részsorozatokat kiválasztva már tud működni.

Bolzano–Weierstrass-tételkör

A lap 2008. május 20., 22:11-kori változata

Tartalomjegyzék

Sorozatkompaktság és B--W-tétel

Az egyváltozós eset

Borel–Lebesgue-tétellel

Többváltozós eset

Nézetek

Személyes eszközök

Navigáció

Keresés

Eszközök