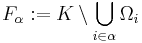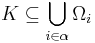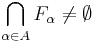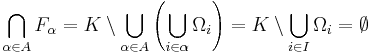Bolzano–Weierstrass-tételkör
A Bolzano–Weierstrass-tételkör és a hozzá kapcsolódó állítások Rn jellegzetes topologiai tulajdonságaira mutatnak rá. Lényegében a korlátos és zárt halmazok kompaktságáról szólnak.
Tartalomjegyzék |
Sorozatkompaktság és B–W-tétel
A Bolzano–Weierstrass-tétel az úgy nevezett sorozatkompaktság fogalmával kapcsolatban kulcsfontosságú tényre mutat rá. Az említett fogalom a következő.
Egy K részhalmaz sorozatkompakt RN-ben (vagy még általánosabban egy M metrikus térben), ha minden a K-ban haladó sorozatból kiválasztható K-beli határértékű konvergens részsorozat. Jelekben:
- K sorozatkompakt
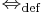
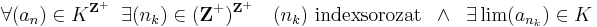
A konvergens részsorozatra vonatkozó tétel RN-ben:
BOLZANO–WEIERSTRASS-FÉLE KIVÁLASZTÁSI TÉTEL. Korlátos sorozatnak van konvergens részsorozata.
Bizonyítását külön nézzük az egy és a többváltozós esetre.
Kompakt halmazok és H–B-tétel
A metrikus terek analízisének egyik jelentő eredménye, hogy a sorozatkompaktság és a topologikus kompaktság fogalma egybeeseik. Alább a topologikus kompaktságal és az őzt motiváló tétellel, a Heine–Borel-tétellel (vagy más elnevezéssel Borel–Lebesgue-tétellel) foglalkozunk.
Kompakt egy K halmaz, ha minden nyílt halmazrendszerből, melynek uniója lefedi K-t kiválasztható véges sok nyílt halmaz is, melyek véges uniója még mindig lefedi K-t.
HEINE–BOREL-TÉTEL. RN-ben korlátos és zárt halmaz kompakt.
Cantor-tétellel
A Cantor-féle közösrész tétel egy ekvivalens megfogalmazását fogjuk használni. Eszerint, ha 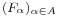 R-beli korlátos és zárt halmazok olyan nemüres rendszere, hogy minden α, β ∈ A indexre létezik olyan γ ∈ A index, hogy Fγ ⊆ Fα∩F</sub>β</sub> (azaz lefelé irányított), akkor az
R-beli korlátos és zárt halmazok olyan nemüres rendszere, hogy minden α, β ∈ A indexre létezik olyan γ ∈ A index, hogy Fγ ⊆ Fα∩F</sub>β</sub> (azaz lefelé irányított), akkor az 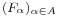 halmazrendszer metszete nem üres.
halmazrendszer metszete nem üres.
Jelölje A az I véges részhalmazainak halmazát és legyen tetszőleges α ∈ A-ra:
Ekkor a 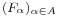 halmazrendszer olyan, hogy minden eleme korlátos és zárt R-ben és tetszőleges α, β ∈ A-ra a γ := α U β elem olyan, hogy Fγ ⊆ Fα∩F</sub>β</sub>. A tételt azt igazolná, ha belátnánk, hogy van olyan α∈A, hogy Fα ≠ ∅, ugyanis ekkor
halmazrendszer olyan, hogy minden eleme korlátos és zárt R-ben és tetszőleges α, β ∈ A-ra a γ := α U β elem olyan, hogy Fγ ⊆ Fα∩F</sub>β</sub>. A tételt azt igazolná, ha belátnánk, hogy van olyan α∈A, hogy Fα ≠ ∅, ugyanis ekkor
teljesülne.
Ha 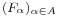 minden eleme nemüres volna, akkor a Cantor-axióma fenti alakjából következne, hogy
minden eleme nemüres volna, akkor a Cantor-axióma fenti alakjából következne, hogy
ami ellentmondás, hiszen 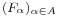 definíciójából és a halmazkivonásra vonatkozó de-Morgan-szabályból következik, hogy
definíciójából és a halmazkivonásra vonatkozó de-Morgan-szabályból következik, hogy
Tehát van 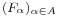 -nak olyan eleme, mely üres, és az ezt indexező α∈A-val a
-nak olyan eleme, mely üres, és az ezt indexező α∈A-val a 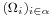 a kívánt tulajdonságú lefedés lesz.
a kívánt tulajdonságú lefedés lesz.
Bolzano–Weierstrass-tétellel
Mivel R teljesíti a második megszámlálhatósági kritéruimot, azaz van megszámlálható környezetbázisa (például a racionális végpontú nyílt intervallumok ilyet alkotnak), a K korlátos és zárt halmazt lefedő rendszerből kiválasztható megszámlálható részlefedés. Legyen ez (Ωi)i=1∞. Definiálunk egy K-ban haladó (xn) sorozatot. Ha Ω1 lefedi K-t, akkor megtaláltuk a véges részlefedést. Ha Ω1 nem fedi le K-t, legyen x1 ∈ K \ Ω1. Ha Ω1 ∪ Ω2 már lefedi K-t, akkor szintén megtaláltuk a véges részlefedést. Ha nem, legyen x2 ∈ K \ (Ω1 ∪ Ω2). Így folytatva biztos lesz olyan n, hogy (Ωi)i=1n már lefedi K-t. Tegyük fel ugyanis, hogy nem fedné le. Akkor (xn) egy végtelen, K-ban haladó sorozat lenne, aminek a Bolzano–Weierstrass-tétel szerint lenne u ∈ K sűrűsödési pontja. Mivel (Ωi)i=1∞ lefedi K-t ezért u-t is tartalmazza egy Ωm nyílt halmaz. u-nak van Ωm-be eső nyílt környezete, és ebben a környezetben végtelen sok (xn)-beli tag. (xn) konstrukciója szerint minden n-re (Ωi)i=1n-ben csak véges sok tag lehet. Ez azonban ellentmond annak, hogy már magában Ωm-ben is végtelen sok tag van.
Tehát a véges nyílt lefedés kiválasztásának fenti konstrukciója véges sok lépésben véget ér (bár, hogy mi lesz ez a szám, előre nem tudjuk megmondani sehogyan sem; sőt, már magát (Ωi)i=1∞ sem fogjuk tudni megadni konstruktívan, kézzelfogaható módon).
Kapcsolatok
Rn-ben tehát a kompaktság ugyanaz, mint a sorozatkompaktság.
Rn véges dimenziószáma nagyon lényegesen hozzájárul a fenti tételek fennállásához. Általában (Haussdorf-térben) kompakt halmaz korlátos és zárt. Ám, van olyan végtelen dimenziós normált tér, melyben zárt és korlátos halmaz nem kompakt. Legyen ugyanis 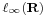 a korlátos sorozatok tere. A téren a norma a suprémum:
a korlátos sorozatok tere. A téren a norma a suprémum:
Ekkor a
"gömb" nem kompakt.
Hasonló furcsaságokat jelentkeznek a p-edik hatványon szummálható sorozatok 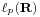 terében is. Számunkra esetleg a véges sorösszeggel rendelkező
terében is. Számunkra esetleg a véges sorösszeggel rendelkező 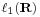 tér bír jelentőséggel.
tér bír jelentőséggel.