Bolzano–Weierstrass-tétel
Bolzano–Weierstrass-tételnek több, de egymáshoz szorsan kapcsolódó tételt neveznek az analízisben. Egyfelől az RN-beli sorozatok elméletében rámutathatunk, hogy minden korlátos sorozatnak van konvergens részsorozata, ezt néha Bolzano–Weierstrass-féle kiválasztási tételnek nevezik. Másrészt zárt és korlátos RN-beli halmazban haladó sorozatnak van a halmazbeli határértékkel rendelkező részsorozata. Harmadrészt RN-beli végtelen, korlátos sorozatnak van torlódási pontja.
Tartalomjegyzék |
Bolzano–Weierstrass-féle kiválasztási tétel
RN-ben korlátos sorozatnak van konvergens részsorozata.
Az egyváltozós eset
R-ben ehhez a tételhez még a következő kommentárt fűzhetjük. Egy valós számsorozatnak, ha nem korlátos, biztosan van sűrűsögési pontja, azaz olyan pont, melynek minden kipontozott környezetében végtelen sok elem van. Ez amiatt van, hogy az egydimeniós esetben értelmezhető az, hogy a +∞ és –∞ értékek sűrűsödési helyek legyenek, éspedig a +∞ gömbi környezetei az
alakú intervallumok, ahol r pozitív szám (melyet a környezet sugarának nevezünk). Világos, hogy nem-korlátos sorozatra a két végtelen érték valamelyike sűrűsödési hely lesz.
Ennél érdekesebb kérdés, hogy van-e sűrűsödési pontja egy korlátos sorozatnak. Erre majdnem triviális indoklást a lenti Borel–Lebesgue-tétel szerinti bizonyítás ad. Jobban rávilágít azonban az indokra a csúcselemes vagy a felső és alső határértékeket felhasználó igazolási mód.
Bizonyítás csúcselemmel
Belátjuk, hogy minden valós sorozatból kiválasztható monoton részsorozat.
Ehhez először vezessük be a csúcselem fogalmát. ak-t csúcselemnek nevezzük, ha minden n > k esetén 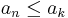 . (Vagyis azokat az elemeket nevezzük így, amelyeknél a nagyobb indexű elemek között nincs nagyobb.)
. (Vagyis azokat az elemeket nevezzük így, amelyeknél a nagyobb indexű elemek között nincs nagyobb.)
Ekkor két eset lehetséges:
- Végtelen sok csúcselem van a sorozatban. Ha
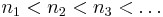 indexek, melyekre
indexek, melyekre 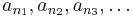 csúcselemek, akkor ez utóbbi sorozat nyilvánvalóan monoton csökkenő.
csúcselemek, akkor ez utóbbi sorozat nyilvánvalóan monoton csökkenő.
- Véges sok csúcselem van a sorozatban. Vagyis létezik n0, hogy minden
 esetén an nem csúcselem.
esetén an nem csúcselem.
- De
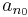 nem csúcselem, vagyis létezik n1 > n0, hogy
nem csúcselem, vagyis létezik n1 > n0, hogy 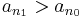 .
.
- De
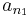 nem csúcselem, vagyis létezik n2 > n1, hogy
nem csúcselem, vagyis létezik n2 > n1, hogy 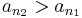 stb.
stb.
Ekkor viszont 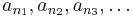 nyilván szigorúan monoton növő sorozat.
nyilván szigorúan monoton növő sorozat.
Vagyis minden sorozatnak van monoton részsorozata. De a mi sorozatunk egyben korlátos is, márpedig korlátos monoton sorozat konvergens.
Bizonyítás Borel–Lebesgue-tétellel
Azt fogjuk belátni, hogy a sorozatnak van sűrűsödési pontja, azaz olyan pont, melynek minden nyílt környezetében van végtelen sok sorozatbeli elem. Ekkor ugyanis már kiválasztható az u sűrűsödési helyhez konvergáló részsorozat: minden n-re:
ahol (δn) egy szigorúan monoton csökkenő nullsorozat.
Legyen [a,b] olyan korlátos és zárt intervallum, mely lefedi a sorozatot. Tegyük fel indirekt módon, hogy an-nek nincs sűrűsödési helye. Ekkor minden x ∈ [a,b]-nek létezik olyan nyílt környezete, melyben csak véges sok sorozatbeli elem van. Az [a,b] intervallum ezen halmazokból álló nyílt lefedéséből kiválasztható véges sok, mely még mindig lefedés, éspedig a Borel–Lebesgue-tétel miatt. Tehát a sorozatnak összesen véges sok szor véges sok, azaz véges sok eleme eshet [a,b]-be, ami ellentmond annak, hogy a sorozatnak végtelen sok tagja van és ez mind [a,b]-ben van.
Intervallumfelezéssel
Legyen (an) korlátos számsorozat, ekkor (an) lefedhető valamely [α,β] korlátos és zárt intervallummal. Intervallumfelezéses eljárással rekurzív módon definiálni fogunk egymásba skatulyázott, nullához tartó hosszúságú intervallumok (Ik) sorozatát a következőképpen.
- I0:=[α0,β0]:=[α,β]
- Ha k természetes szám, és Ik=[αk,βk] már definiálva van, akkor osszuk két egyenlő hosszúságú részre: Ik = [αk,ck] U [ck,βk]. Valamelyikben a sorozatnak bizonyosan végtelen sok különböző indexű tagja van (ellenkező esetben ugyanis nem beszélhetnénk végtelen sorozatról). Természetesen előfordulhat, hogy mindkettőbe végtelen sok tag esik. A meghatározottság kedvéért legyen Ik+1 a két fél közül az az intervallum, melyben végtelen sok különböző indexű tag esik és ezek közül a „jobboldali” félintervallum. (Ezzel azt értük el, hogy az intervallumsorozat minden tagjában lesz sorozatbeli elem.)
A Cantor-axióma (vagy Cantor-féle közöspont tétel) szerint, mely az egymásba skatulyázott intervallumokról szól az (Ik) intervalumsorozatnak létezik egyetlen közös pontja, legyen ez c.
Megállapíthatjuk, hogy minden k természetes számra végtelen sok olyan i index (természetes szám) van, hogy ai ∈ Ik, tehát minden k természetes számra igaz, hogy
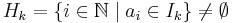 .
.
Megjegyezzük, hogy a természetes számok jólrendezési tulajdonsága miatt ezeknek a nemüres halmazoknak van minimális elemük. Ezekből a halmazokból kell kiválasztanunk egy (ik) indexsorozatot (tehát egy szigorúan monoton növekvő sorozatot). Ezt szintén rekurzióval tesszük.
- i0:=min H0
- Ha már ik definiálva van minden k-nél nem nagyobb természetes számra, akkor legyen ik+1 az a szám, amelyik nagyobb az eddig definiált véges sok elemtől és a legkisebb ilyen elem Hk+1-ben.
Ekkor az
sorozat c-hez konvergál. QED
Megjegyzések. Vegyük észre, hogy bár kiválasztásról van szó, mégsem kellett használnunk a kiválasztási axiómát, hiszen a természetes számokat a szokásos rendezés jólrendezi, így mindig konstruktívan (egyértelműen megnevezve) tudtunk kijelölni egy elemet a nemüres részhalmazaiból.
A másik hasznos tulajdonsága a bizonyításnak, hogy kis módosítással többet is állíthatunk segítségével. Ha a fenti konstrukcióban a végtelen sorozatelemet tartalmazó intevallumok közül mindig a felsőt választjuk, akkor az intervallumok közös pontja a sorozat felső határértéke, azaz a legnagyobb sűrűsödési hely
lesz. Ha mindig az alsó intervallumot, akkor a legkisebb sűrűsödési helyhez jutunk azaz
-hez.
Többváltozós eset
Itt a csúcselemes bizonyítás nem működik abban az értelmeben, hogy közvetlenül nem hivatkozhatunk rájuk, mert nincs RN-ben a műveletekkel kompatibilis rendezés. Gondolhatnók arra is, hogy komponensenként használjuk az egydimenziós B–W-tételt. Ezzel a következő a probléma. Világos, hogy létezik minden projekciósorozatra egy-egy részsorozat, mely konvergens. Ám ebből egyáltalán nem következtethetünk arra, hogy ezek metszetéből kiválasztható részsorozat. Ellenpéldaként vegyünk egy R2-ben haladó sorozatot. Tegyük fel, hogy (szerencsétlen módon) az egydimenziós B–W-tétel az első komponensek sorozatából a páros indexűeket, a második komponensek közül a páratéan indexűeket választja ki. Ekkor a kétdimenziós sorozatnak nincs olyan részsosozata, mely a komponensorozatok közös indexeikből válaszható ki, tekintve, hogy a közös indexen halmaza üres.
A fentiek miatt olyan módon kell konvergens részsorozatokat kiválasztanunk, mely bizonyosan végtelen sok közös indexel rendelkeznek. A konstrukció a következő.
Bizonyítás
Legyen
egy N komponensű sorozat, mely korlátos RN-ben. Ekkor a komponenssorozatok is korlátosak. Az egydimenziós B–W-tétel szerint az
sorozathoz létezik σ1 indexsorozat úgy, hogy az
konvergens részsorozat. Hasonlóképpen, de a
sorozatnak is van
konvergens részsorozata. Megállapíthatjuk, hogy a
sorozat szintén konvergens, mert konvergens sorozat részsorozata. Ugyanígy léteznek σ1, σ2, ..., σN indexsorozatok, hogy a
sorozatok mind konvergensek és így tetszőleges k=1...N-re
is az, ami pontosan azt jelenti, hogy az
sorozat komponensenként konvergens, azaz konvergens. A
tehát olyan indexsorozat, mely konvergens részsorozatot választ ki (an)-ből.
B–W-tétel mint a B–W-féle kiválasztási tétel következménye
Az előbbi tétel múlhatatlan fontosságú következménye az amit sokhelyütt szintén Bolzano–Weierstrass-tételnek neveznek vagyis, hogy egy R-beli halmaz pontosan akkor korlátos és zárt, ha kompakt. Itt egészen pontosan sorozatkompaktságról van szó, azaz arról, amikor egy tetszőleges H ⊆ R halmazra teljesül, hogy minden H-beli értékeket felvevő sorozatnak van H-beli határértékű konvergens részsorozata.
B–W-tétel – Egy H ⊆ R halmaz akkor és csak akkor korlátos és zárt, ha sorozatkompakt.
Bizonyítás. Először tegyük fel, hogy H korlátos és zárt. Ekkor a Bolzano–Weierstrass-féle kiválasztási tételből következik, hogy minden H-ban haladó sorozatnak – minthogy ezeket lefedi a korlátos H – létezik konvergens rélszsorozata. H zártságából pedig az következik, hogy minden H-beli értékeket felvevő konvergens sorozat határértéke szintén H-beli, amivel az állítás első fele bebizonyosodott.
Másrészt legyen H sorozatkompakt. Ha nem lenne korlátos, akkor tetszőleges n természetes számra
lenne, és így a kiválasztási axióma segítségével definiálhatunk egy (sn) sorozatot, melynek elemei rendre Hn-beliek. Ekkor minden n természetes számra sn > n, és így tetszőleges (kn) indexsorozatra (szig. mon. növekvő) |s(kn)| > kn > n, ami azt jeleni, hogy (sn)-nek nincs konvergens részsorozata.
A zártsághoz tekintsük H lezártjának egy h elemét. Ekkor létezik h határértékkel H-beli elemekből konvergens sorozat, melyből a sorozatkompaktság miatt szükségképpen h ∈ H következik. QED
A tétel párja a Borel–Lebesgue-féle lefedési tétel, mely szerint korlátos és zárt R-beli halmaz minden nyílt lefedéséből kiválasztható véges részlefedés (korlátos és zárt R-beli halmaz kompakt).
Ellenpélda végtelen dimenzióra
A tétel végtelen dimenziós esetben nem igaz. Vegyük példul a korlátos valós függvények
terében a szuprémumnormát:
és a belőle definiálható távolságot. Ebben az esetben a páratlan gyökkitevőjű gyökfüggvények
sorozata nem konvergens. Ez amiatt van, hogy az itteni konvergenciafogalom ugyanaz, mint a függvénysorozatok egyenletes konvergenciájának fogalma. Bár ez a függvénysorozat pontonként konvergál a szignumfüggvényhez, de a sorozat a szignumfüggvény minden környezetéből kilép. Emiatt még az is igaz, hogy egyetlen részsorozta sem lehet konvergens (azaz egyenletesen konvergens), holott a függvénysorozat maga korlátos (u.is. belefoglalható az azonosan 0 függvény 2 sugarú környezetébe).
Megjegyzés. A tétel azon iránya, mely a sorozatkompaktságot tételezi fel, igaz marad minden metrikus térben.
Példa alkalmazásra
A Bolzano–Weierstrass-tételt felhasználhatjuk például arra is, hogy igazoljuk, hogy R-ben (tehát RN-ben is) minden Cauchy-sorozat konvergens.
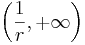
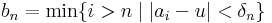
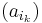
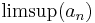
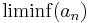
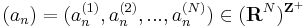
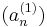
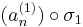
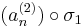
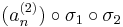
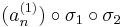

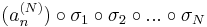
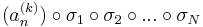
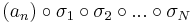
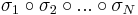
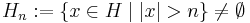
![\mathrm{B}([-1,+1],\mathbf{R})\,](/upload/math/6/f/8/6f81ef1e657e662d5f30dcfba319be40.png)
![||f||=_{\mathrm{def}}\sup\{|f(x)|\mid x\in [-1,+1]\}\,](/upload/math/9/e/c/9ec0abff769966a02d1869c5efc9881e.png)
![f_n=\sqrt[2n+1]{.\;}\quad\quad (f_n(x)=\sqrt[2n+1]{x})](/upload/math/6/8/1/68142b19ef9f58a8e151b2ea4973d681.png)