Szerkesztő:Mozo/ A2 bizonyítások
Többváltozós B–W-tétel
- Lásd még:Bolzano–Weierstrass-tétel
A többdimenziós (de nem végtelendimenziós) esetben a csúcselemes bizonyítás nem működik abban az értelmeben, hogy közvetlenül nem hivatkozhatunk rájuk, mert nincs RN-ben a műveletekkel kompatibilis rendezés. Gondolhatnók arra is, hogy komponensenként használjuk az egydimenziós B–W-tételt. Ezzel a következő a probléma. Világos, hogy létezik minden projekciósorozatra egy-egy részsorozat, mely konvergens. Ám ebből egyáltalán nem következtethetünk arra, hogy ezek metszetéből kiválasztható részsorozat. Ellenpéldaként vegyünk egy R2-ben haladó sorozatot. Tegyük fel, hogy (szerencsétlen módon) az egydimenziós B–W-tétel az első komponensek sorozatából a páros indexűeket, a második komponensek közül a páratéan indexűeket választja ki. Ekkor a kétdimenziós sorozatnak nincs olyan részsosozata, mely a komponensorozatok közös indexeikből válaszható ki, tekintve, hogy a közös indexen halmaza üres.
A fentiek miatt olyan módon kell konvergens részsorozatokat kiválasztanunk, mely bizonyosan végtelen sok közös indexel rendelkeznek. A konstrukció a következő.
Bizonyítás
Legyen
egy N komponensű sorozat, mely korlátos RN-ben. Ekkor a komponenssorozatok is korlátosak. Az egydimenziós B–W-tétel szerint az
sorozathoz létezik σ1 indexsorozat úgy, hogy az
konvergens részsorozat. Hasonlóképpen, de a
sorozatnak is van
konvergens részsorozata. Megállapíthatjuk, hogy a
sorozat szintén konvergens, mert konvergens sorozat részsorozata. Ugyanígy léteznek σ1, σ2, ..., σN indexsorozatok, hogy a
sorozatok mind konvergensek és így tetszőleges k=1...N-re
is az, ami pontosan azt jelenti, hogy az
sorozat komponensenként konvergens, azaz konvergens. A
tehát olyan indexsorozat, mely konvergens részsorozatot választ ki (an)-ből.
Ellenpélda végtelen dimenzióra
A tétel végtelen dimenziós esetben nem igaz. Vegyük példul a korlátos valós függvények
terében a szuprémumnormát:
és a belőle definiálható távolságot. Ebben az esetben a páratlan gyökkitevőjű gyökfüggvények
sorozata nem konvergens. Ez amiatt van, hogy az itteni konvergenciafogalom ugyanaz, mint a függvénysorozatok egyenletes konvergenciájának fogalma. Bár ez a függvénysorozat pontonként konvergál a szignumfüggvényhez, de a sorozat a szignumfüggvény minden környezetéből kilép. Emiatt még az is igaz, hogy egyetlen részsorozta sem lehet konvergens (azaz egyenletesen konvergens), holott a függvénysorozat maga korlátos (u.is. belefoglalható az azonosan 0 függvény 2 sugarú környezetébe).
Megjegyzés. A tétel azon iránya, mely a sorozatkompaktságot tételezi fel, igaz marad minden metrikus térben.
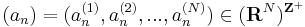
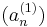
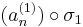
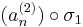
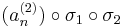
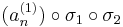

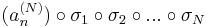
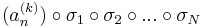
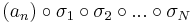
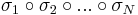
![\mathrm{B}([-1,+1],\mathbf{R})\,](/upload/math/6/f/8/6f81ef1e657e662d5f30dcfba319be40.png)
![||f||=_{\mathrm{def}}\sup\{|f(x)|\mid x\in [-1,+1]\}\,](/upload/math/9/e/c/9ec0abff769966a02d1869c5efc9881e.png)
![f_n=\sqrt[2n+1]{.\;}\quad\quad (f_n(x)=\sqrt[2n+1]{x})](/upload/math/6/8/1/68142b19ef9f58a8e151b2ea4973d681.png)