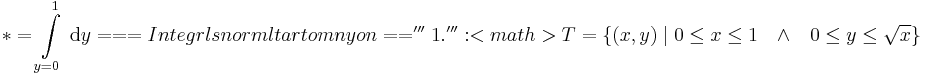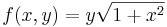Matematika A2a 2008/10. gyakorlat
A MathWikiből
(Változatok közti eltérés)
Mozo (vitalap | szerkesztései) (→Szakadásos függvény integrálja téglalaptartományon) |
Mozo (vitalap | szerkesztései) (→Szakadásos függvény integrálja téglalaptartományon) |
||
| 23. sor: | 23. sor: | ||
'''2.''' | '''2.''' | ||
| − | :<math>f(x,y)=\left\{\begin{matrix}\frac{1}{\sqrt{x | + | :<math>f(x,y)=\left\{\begin{matrix}\frac{1}{\sqrt{x+y^2}}, & \mathrm{ha} & x+y^2 > 0\\ |
| − | 0, & \mathrm{ha}& x | + | 0, & \mathrm{ha}& x+y^2\leq 0\end{matrix}\right.</math> |
| − | :<math> T= | + | :<math> T=[0,1]\times [0,1]</math> |
:<math>\int\limits_T f=?</math> | :<math>\int\limits_T f=?</math> | ||
Az | Az | ||
| − | :<math>y=\pm\sqrt{ | + | :<math>y=\pm\sqrt{-x}</math> |
| − | pontokban a függvénynek szakadása | + | pontokban a függvénynek szakadása, ahol ''x'' nulla vagy negatív, ráadásul nem is korlátos, így nem inregrálható. Ellenben a [δ,1]×[0,1] téglalapon létezik integrája minden δ > 0 esetben és az egységkockán improprius integrálható, mert |
| + | :<math>0\leq f(x,y)\leq\frac{1}{\sqrt{x}}\,</math> | ||
| + | ami utóbbi impróprius integrálható. | ||
| + | :<math>\int\limits_{x=\delta}^{1}\int\limits_{y=0}^{1}\frac{1}{\sqrt{x+y^2}}\,\mathrm{d}x\,\mathrm{d}y=*</math> | ||
| + | ::<math>F(x)=\int\limits_{y=0}^{1}\frac{1}{\sqrt{x+y^2}}\,\mathrm{d}y=[2\sqrt{x+y^2}]_{x=0}^1=2(\sqrt{y^2+1}-\sqrt{y^2})</math> | ||
| + | :<math>*=\int\limits_{y=0}^{1}\,\mathrm{d}y= | ||
==Integrálás normáltartományon== | ==Integrálás normáltartományon== | ||
A lap 2009. május 1., 16:32-kori változata
- Ez az szócikk a Matematika A2a 2008 alszócikke.
Szakadásos függvény integrálja téglalaptartományon
1.
A függvény csak egy pontban szakad és korlátos, így integrálható.
F a [0,1]-en nincs értelmezve, mert 0-ban szakadása van, de
ami imprópriusan integrálható:
Hiszen tudjuk:
2.
Az
pontokban a függvénynek szakadása, ahol x nulla vagy negatív, ráadásul nem is korlátos, így nem inregrálható. Ellenben a [δ,1]×[0,1] téglalapon létezik integrája minden δ > 0 esetben és az egységkockán improprius integrálható, mert
ami utóbbi impróprius integrálható.
| 9. gyakorlat | 11. gyakorlat |
![T=[0,1]\times[0,1]](/upload/math/3/a/b/3ab1c06a3127ca44d6b7adcdf4ffd3aa.png)
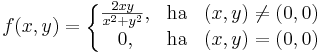
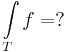
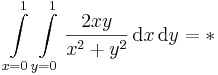
![F(x)=\int\limits_{y=0}^{1}\frac{2xy}{x^2+y^2}\,\mathrm{d}y=\left[x\mathrm{ln}(x^2+y^2)\right]_{y=0}^1=x\mathrm{ln}(x^2+1)-x\mathrm{ln}(x^2)](/upload/math/4/7/a/47a031aca3f54a82649d7b79b0f59330.png)
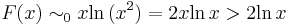
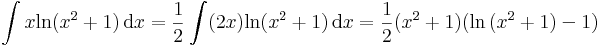
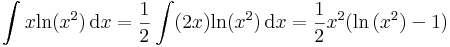
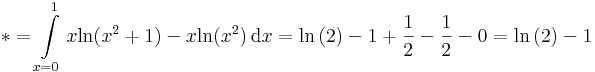
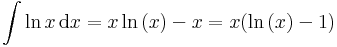
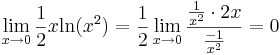
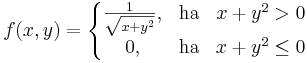
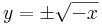
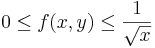

![F(x)=\int\limits_{y=0}^{1}\frac{1}{\sqrt{x+y^2}}\,\mathrm{d}y=[2\sqrt{x+y^2}]_{x=0}^1=2(\sqrt{y^2+1}-\sqrt{y^2})](/upload/math/a/6/c/a6c2d51aa27b19deb412bf1b980389c7.png)