Matematika A2a 2008/11. gyakorlat
A MathWikiből
- Ez az szócikk a Matematika A2a 2008 alszócikke.
Totális és folytonos parciális deriválhatóság
Deriválható-e az
függvény az origóban? Folyt. diff.-e, létezik-e a gradiens, létezik-e a Jacobi-mátrix ott?
A deriválhatóság:
ugyanis
Tehát nem folyt diff, mert ha az lenne, akkor deriválható is lenne (egy környzetben létezik a derivált!). Jacobi van, gradiens nincs, mert az a differenciál leképezés skalárinvariánssa lenne ( az az m vektor, melyet az Ax=m x definiál, de nincs alkalmas A, így nincs alkalmas m).
x definiál, de nincs alkalmas A, így nincs alkalmas m).
Kettősintegrál
T: a (0,0), (0,1), (1,0) csúcspontú háromszög.
| 10. gyakorlat | 12. gyakorlat |
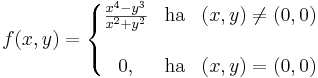
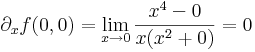
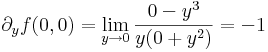
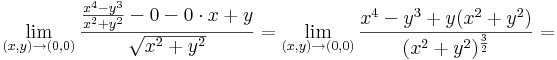
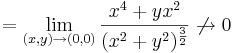
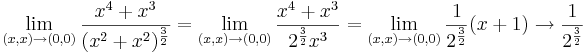
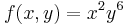
![\int\limits_{x=0}^1\int\limits_{y=0}^{1-x} x^2y^6\,\mathrm{d}x\mathrm{d}y=\int\limits_{x=0}^1\frac{1}{7}[x^2y^7]_{y=0}^{1-x}\,\mathrm{d}x=\int\limits_{x=0}^1\frac{1}{7}x^2(1-x)^7\,\mathrm{d}x=?](/upload/math/d/b/0/db02d521d71809744e6ebc04e9dbce6f.png)
![\int\limits_{y=0}^1\int\limits_{x=0}^{1-y} x^2y^6\,\mathrm{d}x\mathrm{d}y=\int\limits_{y=0}^1\frac{1}{3}[x^3y^6]_{x=0}^{1-y}\,\mathrm{d}x=\int\limits_{x=0}^1\frac{1}{3}y^6(1-y)^3\,\mathrm{d}y=](/upload/math/8/2/5/82513a630c4b4e4a85bfb922899222a5.png)