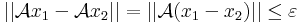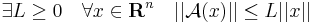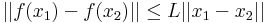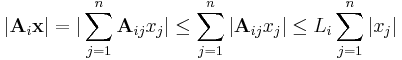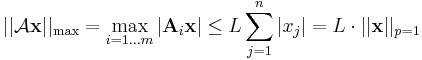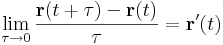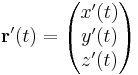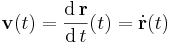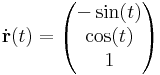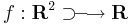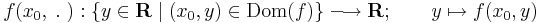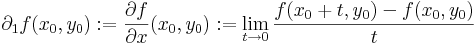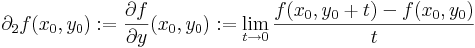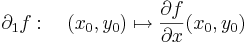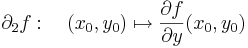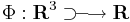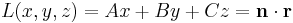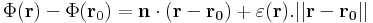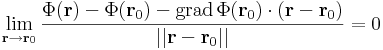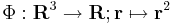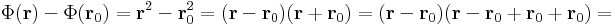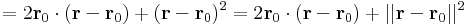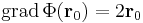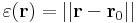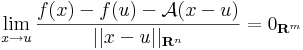Matematika A2a 2008/4. gyakorlat

A MathWikiből

(Változatok közti eltérés)

Ugrás: navigáció, keresés

A lap 2008. március 14., 18:54-kori változata

Ez az szócikk a Matematika A2a 2008 alszócikke.

Tartalomjegyzék

1 Lineáris leképezések folytonossága
2 Deriváltfogalmak Rⁿ-ben
3 Differenciálhatóság

Lineáris leképezések folytonossága

Megjegyzés. A normált terek között ható A lineáris leképezés folytonos, ha a 0-ban folytonos.

Ugyanis, legyen az A: $N 1$ $\to$ $N 2$ lineáris leképezés és tegyük fel, hogy 0-ban folytonos, azaz minden ε>0-ra létezik δ>0, hogy minden x ∈ B_δ(0)-ra Ax ∈ B_ε(0).

Most ha ε > 0 tetszőleges és $x 1$ és $x 2$ $N 1$ -beliek is tetszőlegesek, akkor

$||\mathcal{A}x_1-\mathcal{A}x_2||=||\mathcal{A}(x_1-x_2)||\leq\varepsilon$

amennyiben $x 1$ - $x 2$ ∈ B_δ(0), ahol δ a 0-beli folytonosság által az ε-hoz tartozó δ.

Tétel. A : Rⁿ $\to$ R^m lineáris leképzés folytonos, sőt:

$\exists L\geq 0\quad\forall x\in \mathbf{R}^n\quad||\mathcal{A}(x)||\leq L||x||$

Megjegyzés. Ez azt is jelenti, hogy egy ilyen leképezés Lipschitz-függvény. Az f: Rⁿ ⊃ $\to$ R^m függvényt Lipschitz-függvénynek nevezük, ha létezik L nemnegatív szám, hogy minden $x 1$ és $x 2$ Dom(f)-belire:

$||f(x_1)-f(x_2)||\leq L||x_1-x_2||$

Világos, hogy ez lineáris leképezésre ekvivalens a tételbeli megfogalmazással.

Bizonyítás. Vegyük az A szetenderd bázis beli mátrixát. Ekkor A(x)=A $\cdot$ x. Így A minden A_i sorára

$|\mathbf{A}_i\mathbf{x}|=|\sum\limits_{j=1}^{n}\mathbf{A}_{ij}x_j|\leq\sum\limits_{j=1}^{n}|\mathbf{A}_{ij}x_j| \leq L_i\sum\limits_{j=1}^{n}|x_j|$

ahol $L i$ rögzített i mellett a {|A_i,j|} _j=1...n számok maximuma. Ha most vesszük L = max { $L i$ }-t is, akkor

$||\mathcal{A}\mathbf{x}||_\max=\max_{i=1...m}|\mathbf{A}_i\mathbf{x}|\leq L\sum\limits_{j=1}^{n}|x_j|=L\cdot ||\mathbf{x}||_{p=1}$

is teljesül, azaz a kép maximumnormája felülbecsülhető L-szer a vektor norma-1 szerinti normájával. A normák ekvivalenciája miat pedig alkalmas L-re minden normára igaz.

Deriváltfogalmak Rⁿ-ben

A többdimenziós terekben több természetes általánosítására lelhetünk az egyváltozós függvények deriváltfogalmának. A következőkben konkrét esetekt nézünk.

Görbék

A görbék lényegében egyváltozós vektorértékű függvények: r: $I$ $\to$ R³; t $\mapsto$ r(t). Ezekre a deriváltat definiáló határérték válzatlan alakban írható:

$\lim\limits_{\tau\to 0}\frac{\mathbf{r}(t+\tau)-\mathbf{r}(t)}{\tau}=\mathbf{r}'(t)$

feltéve, hogy ez a határérték egyáltalán létezik az R³ normájában. A geometriai jelentésből az is következik, hogy a fenti határérték ugyanúgy a szelők határértékét, azaz az érintőt adják, mint az egyváltozós függvények esetén. Ekkor t jelentése: idő. A komponensenkénti határértékképzés miatt világos, hogy

$\mathbf{r}'(t)=\begin{pmatrix}x'(t)\\y'(t)\\z'(t)\end{pmatrix}$

Ezt még a görbe idő szerinti paraméterezésének is nevezzük, melynek fenti deriváltja a sebességet adja és vessző helyett ponttal is jelöljük a deriváltat:

$\mathbf{v}(t)=\frac{\mathrm{d}\,\mathbf{r}}{\mathrm{d}\,t}(t)=\dot{\mathbf{r}}(t)$

Példa.

$\mathbf{r}:[0,4\pi]\longrightarrow\mathbf{R}^3;\quad \mathbf{r}(t)=\begin{pmatrix}\cos(t)\\\sin(t)\\t\end{pmatrix}$

set size 0.5,0.5

set parametric set urange [0:4*pi] unset colorbox unset key unset xtics unset ytics unset ztics

splot cos(u),sin(u),u

egy spirál paraméterezése. A deriváltja:

$\dot{\mathbf{r}}(t)=\begin{pmatrix}-\sin(t)\\\cos(t)\\1\end{pmatrix}$

amiből látszik, hogy az [xy] síkra vett vetülete egy egyenletes körmozgás, a z tengelyre eső vetülete pedig egy egyenesvonalú egyenletes mozgás.

Felületek

Ha adott az

$f:\mathbf{R}^2\supset\!\longrightarrow\mathbf{R}$

kétváltozós függvény, akkor adott ( $x 0$ , $y 0$ ) ∈ Dom(f) pont körül ebből származtathatunk két egyváltozós függvényt:

$f(\;.\;,y_0):\{x\in \mathbf{R}\mid (x,y_0)\in\mathrm{Dom}(f)\}\longrightarrow \mathbf{R};\quad\quad x\mapsto f(x,y_0)$

$f(x_0,\;.\;):\{y\in \mathbf{R}\mid (x_0,y)\in\mathrm{Dom}(f)\}\longrightarrow \mathbf{R};\quad\quad y\mapsto f(x_0,y)$

Ezeket parciális függvényeknek nevezzük, és ha differenciálhatóak rendre az $x 0$ és az $y 0$ pontokban, akkor a deriváltjuk a parciális deriváltak:

$\partial_1f(x_0,y_0):=\frac{\partial f}{\partial x}(x_0,y_0):=\lim\limits_{t\to 0}\frac{f(x_0+t,y_0)-f(x_0,y_0)}{t}$

$\partial_2f(x_0,y_0):=\frac{\partial f}{\partial y}(x_0,y_0):=\lim\limits_{t\to 0}\frac{f(x_0,y_0+t)-f(x_0,y_0)}{t}$

Geometriailag ezek a ( $x 0$ , $y 0$ ) pontban állított [x,z] síkkal illetve az [yz] síkkal vett metszetgörbék, mint egyváltozós függvények deriváltjai. A parciális deriváltfüggvényeket már mint kétváltozós függvényekként definiáljuk:

$\partial_1 f:\quad(x_0,y_0)\mapsto \frac{\partial f}{\partial x}(x_0,y_0)$

$\partial_2 f:\quad(x_0,y_0)\mapsto \frac{\partial f}{\partial y}(x_0,y_0)$

Példa.

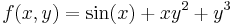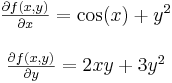
$f(x,y)= \sin(x) + xy^2 + y^3\,$ , akkor $\begin{matrix}\frac{\partial f(x,y)}{\partial x}=\cos(x)+y^2\\ \\\frac{\partial f(x,y)}{\partial y}=2xy + 3y^2\end{matrix}$

Vektor-skalár függvények

Ha adott az

$\Phi:\mathbf{R}^3\supset\!\longrightarrow\mathbf{R}$

vektorváltozós skalárfüggvény, akkor ezt általában szintfelületekkel ábrázolhatjuk. Egy ( $x 0$ , $y 0$ , $z 0$ )elég kis környezetében a függvény -- ha a későbbi értelmeben differenciálható -- akkor jól közelíthető lineáris vektorváltozós skalárfüggvény, tehát valamely

$L(x,y,z)=Ax+By+Cz=\mathbf{n}\cdot\mathbf{r}$

függvény ( $x 0$ , $y 0$ , $z 0$ ) pontba való eltoltjával -- hiszen ennek az ábrázolása síkoksorokkal történik, amik a pont elég kis környzetében már a hibahatáron belül térnek el Φ-től. Ez akkor van, ha a leképezés csak elsőnél magasabbrendű tagokban különbözik a lineáristól, azaz létezik ε(r):Dom(Φ) $\to$ R az r₀ = ( $x 0$ , $y 0$ , $z 0$ )-ban folytonos és ott 0 értéket felvevő függvény, hogy

$\Phi(\mathbf{r})-\Phi(\mathbf{r}_0)=\mathbf{n}\cdot (\mathbf{r}-\mathbf{r_0})+\varepsilon(\mathbf{r}).||\mathbf{r}-\mathbf{r_0}||$

Mindezek miatt értelmes a fenti n vektort mint a lokális viselkedés jellemzőjét, egyfajta diváltat tekinteni. n-et ekkor a Φ leképezés ( $x 0$ , $y 0$ , $z 0$ ) ponthoz tartozó gradiensének nevezzük és tömör definíciója a következő:

$\lim\limits_{\mathbf{r}\to\mathbf{r}_0}\frac{\Phi(\mathbf{r})-\Phi(\mathbf{r}_0)-\mathrm{grad}\,\Phi(\mathbf{r}_0)\cdot(\mathbf{r}-\mathbf{r}_0)}{||\mathbf{r}-\mathbf{r}_0||}=0$

Példa

$\Phi:\mathbf{R}^3\rightarrow\mathbf{R};\mathbf{r}\mapsto\mathbf{r}^2$

függvényt.

Ekkor a gradiensét a következőkből számítjuk ki:

$\Phi(\mathbf{r}) -\Phi(\mathbf{r}_0)=\mathbf{r}^2-\mathbf{r}_0^2=(\mathbf{r}-\mathbf{r}_0)(\mathbf{r}+\mathbf{r}_0)=(\mathbf{r}-\mathbf{r}_0)(\mathbf{r}-\mathbf{r}_0+\mathbf{r}_0+\mathbf{r}_0)=$

$=2\mathbf{r}_0\cdot(\mathbf{r}-\mathbf{r}_0)+(\mathbf{r}-\mathbf{r}_0)^2=2\mathbf{r}_0\cdot(\mathbf{r}-\mathbf{r}_0)+||\mathbf{r}-\mathbf{r}_0||^2$

ahonnan leolvasva:

$\mathrm{grad}\,\Phi(\mathbf{r}_0)=2\mathbf{r}_0$

$\varepsilon(\mathbf{r})=||\mathbf{r}-\mathbf{r}_0||$

mely utóbbi valóban folytonos r₀-ban és értéke itt 0.

Differenciálhatóság

Legyen f: Rⁿ $\supset\!\longrightarrow$ R^m és u ∈ int Dom(f). Azt mondjuk, hogy f differenciálható az u pontban, ha létezik olyan A: Rⁿ $\to$ R^m lineáris leképezés, hogy

$\lim\limits_{x\to u}\frac{f(x)-f(u)-\mathcal{A}(x-u)}{||x-u||_{\mathbf{R}^n}}=0_{\mathbf{R}^m}$

Ekkor A egyértelmű és az f leképezés u-bent beli deriválttenzorának vagy differenciáljának nevezzük és df(u)-val vagy Df(u)-val jelöljük. Ezt a fogalmat néha teljes differenciálnak, totális differenciálnak vagy Fréchet-deriváltnak is mondjuk.

pótló gyakorlat	5. gyakorlat

@@ 1. sor: / 1. sor: @@
 :''Ez az szócikk a [[Matematika A2a 2008]] alszócikke.''
+==Lineáris leképezések folytonossága==
+'''Megjegyzés.''' A normált terek között ható ''A'' lineáris leképezés folytonos, ha a 0-ban folytonos.
+''Ugyanis, '' legyen az ''A'': <math>N_1</math> <math>\to</math> <math>N_2</math> lineáris leképezés és tegyük fel, hogy 0-ban folytonos, azaz minden &epsilon;>0-ra létezik &delta;>0, hogy minden ''x'' &isin; B<sub>&delta;</sub>(0)-ra ''Ax'' &isin; B<sub>&epsilon;</sub>(0).
+Most ha &epsilon; > 0 tetszőleges és <math>x_1</math> és <math>x_2</math> <math>N_1</math>-beliek is tetszőlegesek, akkor
+: <math>||\mathcal{A}x_1-\mathcal{A}x_2||=||\mathcal{A}(x_1-x_2)||\leq\varepsilon</math>
+amennyiben <math>x_1</math>-<math>x_2</math> &isin; B<sub>&delta;</sub>(0), ahol &delta; a 0-beli folytonosság által az &epsilon;-hoz tartozó &delta;.
+'''Tétel.''' ''A'' : '''R'''<sup>n</sup> <math>\to</math> '''R'''<sup>m</sup> lineáris leképzés folytonos, sőt:
+:<math>\exists L\geq 0\quad\forall x\in \mathbf{R}^n\quad||\mathcal{A}(x)||\leq L||x||</math>
+'''Megjegyzés.''' Ez azt is jelenti, hogy egy ilyen leképezés Lipschitz-függvény. Az ''f'': '''R'''<sup>n</sup> &sup;<math>\to</math> '''R'''<sup>m</sup> függvényt Lipschitz-függvénynek nevezük, ha létezik L nemnegatív szám, hogy minden  <math>x_1</math> és <math>x_2</math> Dom(''f'')-belire:
+:<math>||f(x_1)-f(x_2)||\leq L||x_1-x_2||</math>
+Világos, hogy ez lineáris leképezésre ekvivalens a tételbeli megfogalmazással.
+''Bizonyítás.'' Vegyük az ''A'' szetenderd bázis beli mátrixát. Ekkor ''A''('''x''')='''A'''<math>\cdot</math>'''x'''. Így '''A''' minden '''A'''<sub>i</sub> sorára
+: <math>|\mathbf{A}_i\mathbf{x}|=|\sum\limits_{j=1}^{n}\mathbf{A}_{ij}x_j|\leq\sum\limits_{j=1}^{n}|\mathbf{A}_{ij}x_j| \leq L_i\sum\limits_{j=1}^{n}|x_j|</math>
+ahol <math>L_i</math> rögzített i mellett a {|'''A'''<sub>i,j</sub>|} <sub>j=1...n</sub> számok maximuma. Ha most vesszük L = max {<math>L_i</math>}-t is, akkor
+: <math>||\mathcal{A}\mathbf{x}||_\max=\max_{i=1...m}|\mathbf{A}_i\mathbf{x}|\leq L\sum\limits_{j=1}^{n}|x_j|=L\cdot ||\mathbf{x}||_{p=1}</math>
+is teljesül, azaz a kép maximumnormája felülbecsülhető L-szer a vektor norma-1 szerinti normájával. A normák ekvivalenciája miat pedig alkalmas L-re minden normára igaz.
 ==Deriváltfogalmak '''R'''<sup>n</sup>-ben==
 A többdimenziós terekben több természetes általánosítására lelhetünk az egyváltozós függvények deriváltfogalmának. A következőkben konkrét esetekt nézünk.

Matematika A2a 2008/4. gyakorlat

A lap 2008. március 14., 18:54-kori változata

Tartalomjegyzék

Lineáris leképezések folytonossága