Matematika A2a 2008/4. gyakorlat
Mozo (vitalap | szerkesztései) (→Lineáris leképezések folytonossága) |
Mozo (vitalap | szerkesztései) (→Lineáris leképezések folytonossága) |
||
| 150. sor: | 150. sor: | ||
:<math>||\mathcal{A}||_{op}=_{\mathrm{def}}\sup_{\mathbf{x}\ne 0}\frac{||\mathcal{A}\mathbf{x}||}{||\mathbf{x}||}=\sup_{||\mathbf{x}||=1}||\mathcal{A}\mathbf{x}||</math> | :<math>||\mathcal{A}||_{op}=_{\mathrm{def}}\sup_{\mathbf{x}\ne 0}\frac{||\mathcal{A}\mathbf{x}||}{||\mathbf{x}||}=\sup_{||\mathbf{x}||=1}||\mathcal{A}\mathbf{x}||</math> | ||
Ez létezik, mivel x <math>\mapsto</math> ||''A''x|| folytonos a kompakt 0 középpontú, egységsugarú gömbfelületen. | Ez létezik, mivel x <math>\mapsto</math> ||''A''x|| folytonos a kompakt 0 középpontú, egységsugarú gömbfelületen. | ||
| + | ==Differenciálhatóság== | ||
| + | A többváltozós differenciálhatóságot az egyváltozós alábbi átfogalmazásából általánosítjuk: | ||
| + | |||
| + | :<math>\lim\limits_{x\to u}\frac{f(x)-f(u)-m(x-u)}{|x-u|}=0</math> | ||
| + | :<math>\lim\limits_{x\to u+}\frac{f(x)-f(u)-m(x-u)}{x-u}=0\quad\wedge\quad\lim\limits_{x\to u-}\frac{f(x)-f(u)-m(x-u)}{-(x-u)}=0</math> | ||
| + | :<math>\lim\limits_{x\to u+}\left(\frac{f(x)-f(u)}{x-u}-m\right)=0,\quad\wedge\quad\lim\limits_{x\to u-}-\left(\frac{f(x)-f(u)}{x-u}-m\right)=0</math> | ||
| + | :<math>\lim\limits_{x\to u+}\frac{f(x)-f(u)}{x-u}=m,\quad\wedge\quad\lim\limits_{x\to u-}-\frac{f(x)-f(u)}{x-u}=-m</math> | ||
| + | :<math>\lim\limits_{x\to u}\frac{f(x)-f(u)}{x-u}=m</math> | ||
| + | |||
| + | |||
| + | '''Definíció.''' Legyen ''f'': '''R'''<sup>n</sup> <math>\supset\!\longrightarrow</math> '''R'''<sup>m</sup> és ''u'' ∈ int Dom(f). Azt mondjuk, hogy ''f'' '''differenciálható''' az ''u'' pontban, ha létezik olyan ''A'': '''R'''<sup>n</sup> <math>\to</math> '''R'''<sup>m</sup> lineáris leképezés, hogy | ||
| + | :<math>\lim\limits_{x\to u}\frac{f(x)-f(u)-\mathcal{A}(x-u)}{||x-u||_{\mathbf{R}^n}}=0_{\mathbf{R}^m}</math> | ||
| + | Ekkor ''A'' egyértelmű és az ''f'' leképezés ''u''-bent beli '''differenciál'''jának nevezzük és d''f''(''u'')-val vagy D''f''(u)-val jelöljük. Ezt a fogalmat néha ''teljes differenciál''nak, ''totális differenciál''nak vagy ''Fréchet-derivált''nak is mondjuk. | ||
| + | |||
| + | '''Megjegyzés.''' A fenti határérték 0 volta egyenértékű a következő kijelentéssel. Létezik ''A''': ''R'''<sup>n</sup> <math>\to</math> '''R'''<sup>m</sup> lineáris leképezés és ε: Dom(''f'') <math>\to</math> '''R'''<sup>m</sup> függvény, melyre: | ||
| + | : ε folytonos u-ban és ε(u)=0, továbbá | ||
| + | minden ''x'' ∈ Dom(''f'')-re: | ||
| + | : <math>f(x)=f(u)+\mathcal{A}(x-u)+\varepsilon(x)||x-u||</math> | ||
| + | '''Megjegyzés.''' Azt, hogy ''A'' egyértelmű, a következőkkel bizonyíthatjuk. Legyen ''A'' és ''B'' is a mondott tulajdonságú, azaz létezzenek ε és η az ''u''-ban eltűnő és ott folytonos Dom(''f'')-en értelmezett függvények, melyekre teljesül, hogy minden ''x'' ∈ Dom(''f'')-re | ||
| + | :<math>f(x)=f(u)+\mathcal{A}(x-u)+\varepsilon(x)||x-u||</math> | ||
| + | :<math>f(x)=f(u)+\mathcal{B}(x-u)+\eta(x)||x-u||</math> | ||
| + | ezeket kivonva egymásból és használva '''minden''' ''x''-re: | ||
| + | :<math>(\mathcal{A}-\mathcal{B})(x-u)+(\varepsilon(x)-\eta(x))||x-u||=0</math> | ||
| + | így minden x = u + ty értékre is az azonosan nullát kapjuk, ha t pozitív szám, y pedig rögzített nemnulla vektor, azaz minden t-re | ||
| + | :<math>(\mathcal{A}-\mathcal{B})ty+(\varepsilon(u+ty)-\eta(u+ty))||ty||=0</math> | ||
| + | az azonosan 0 függény határértéke t<math>\to</math> 0 esetén szintén nulla: | ||
| + | :<math> 0=\lim\limits_{t\to 0}\frac{(\mathcal{A}-\mathcal{B})(ty)+(\varepsilon(u+ty)-\eta(u+ty))||ty||}{t}=(\mathcal{A}-\mathcal{B})y</math> | ||
| + | hiszen t-t kiemelhetünk és egyszerűsíthetünk és t<math>\to</math> 0 esetén | ||
| + | ε és η nullává válik. | ||
| + | Ez viszont pont azt jelenti, hogy a két lineéris operátor azonosan egyenlő. | ||
| + | |||
| + | ==Jacobi-mátrix== | ||
| + | A d''f''(''u'') lineáris leképezés (<math>e_1</math>,<math>e_2</math>,...,<math>e_n</math>) szetenderd bázisbeli mátrixa legyen: [d''f''(''u'')] = '''A'''. Vizsgáljuk mibe viszi a bázisokat d''f''(''u'') leképezés! | ||
| + | |||
| + | Írjuk fel a definíciót, de az <math>e_1</math> egységvektor mentén tartsunk ''u''-hoz: ''x'' = ''u'' + ''t''<math>e_1</math>. Ekkor | ||
| + | :<math>x-u=te_1\,</math> | ||
| + | ami azért hasznos, mert a | ||
| + | :<math>\mathcal{A}(x-u)=\mathcal{A}(te_1)\,</math> | ||
| + | alakból kiemelhetó t: | ||
| + | :<math>0=\lim\limits_{t\to 0}\frac{f(u+te_1)-f(u)-\mathcal{A}(te_1)}{t}=</math> | ||
| + | :::<math>=\lim\limits_{t\to 0}\frac{f(u+te_1)-f(u)-t.\mathcal{A}(e_1)}{t}=</math> | ||
| + | :::<math>=-\mathcal{A}(e_1)+\lim\limits_{t\to 0}\frac{f(u+te_1)-f(u)}{t}</math> | ||
| + | azaz | ||
| + | :<math>\mathcal{A}(e_1)=\lim\limits_{t\to 0}\frac{f(u+te_1)-f(u)}{t}=\partial_1 f(u)</math> | ||
| + | vagyis ''f'' koordinátafüggvényeinek az első változó szerinti parciális deriváltja az ''u'' pontban. A többi oszlopvektor ugyanígy: | ||
| + | |||
| + | :<math>[\mathrm{d}f(u)]=\mathbf{J}^f(u)=\begin{bmatrix} | ||
| + | \partial_1 f_1(u) & \partial_2 f_1(u) & \dots & \partial_n f_1(u)\\ | ||
| + | \partial_1 f_2(u) & \partial_2 f_2(u) & \dots & \partial_n f_2(u)\\ | ||
| + | \vdots & \vdots & \ddots & \vdots \\ | ||
| + | \partial_1 f_m(u) & \partial_2 f_m(u) & \dots & \partial_n f_m(u)\\ | ||
| + | \end{bmatrix}</math> | ||
| + | amelyet '''Jacobi-mátrix'''nak nevezünk. | ||
| + | |||
| + | '''Következmény.''' Tehát. ha f totálisan differenciálható, akkor parciálisan is differenciálható és a differenciál sztenderd bázisbeli mátrixa a Jacobi-mátrix. | ||
| + | |||
| + | Azaz: | ||
| + | :'''teljes''' differenciálhatóság <math>\Longrightarrow</math> '''parciális''' differenciálhatóság | ||
| + | de ez fordítva már nem igaz: | ||
| + | : '''parciális''' differenciálhatóság <math>\not\Rightarrow</math> '''teljes''' differenciálhatóság | ||
| + | Erre vonatkozik a két alábbi példa. | ||
| + | |||
| + | |||
A lap 2013. szeptember 29., 10:09-kori változata
- Ez az szócikk a Matematika A2a 2008 alszócikke.
Tartalomjegyzék |
Lineáris leképezések
A V1 és V2 vektorterek között ható A leképezést akkor nevezünk lineárisnak, ha teljesül minden λ, μ ∈ R és v, u ∈ V1
A definícióból rögtön következik, hogy a nulla vektor képe nulla:
viszont más elem a V2 nem feltétlenül vétetik föl.
Véges dimenziós terek közti lineáris leképezés a bázis választásával egyértelműen jellemezhető az alábbi mátrixszal.
ahol B = (b1,b2,…,bn) a V1 egy bázisa, C az V2 bázisa, a mátrix oszlopai pedig a B elemeinek 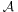 általi képvektoraiból, mint oszlopvektorokból áll. Ha
általi képvektoraiból, mint oszlopvektorokból áll. Ha 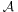 V
V  V típusú, akkor csak
V típusú, akkor csak ![\mbox{ }_{[\mathcal{A}]_B}](/upload/math/1/5/6/156d0043945fe751a951df3818cbfb93.png) -t szokás írni, ha pedig pusztán
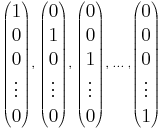
-t szokás írni, ha pedig pusztán ![\mbox{ }_{[\mathcal{A}]}](/upload/math/a/b/0/ab06c27145a3fa90b92cfb08c9e0d4fe.png) -t írnak, akkor az azt jelenti, hogy a Rn sztenderd bázisáról van szó, azaz a
-t írnak, akkor az azt jelenti, hogy a Rn sztenderd bázisáról van szó, azaz a
vektorrendszerről.
Példák
1. Forgatás az origo körül φ szöggel:
Világos, hogy ez invertálható leképezés és az inverze a -φ szögű forgatás.
2. Tükrözés a φ szőgű egyenesre.
Világos, hogy ez is invertálható és inverze saját maga.
Ezek ortogonális transzformációk, azaz a transzponáltjuk az inverzük. Speciálisan a tükrözés szimmetrikus leképezés, mert mátrixa szimmetrikus. Sőt, ezek alkotják a síkon az összes ortogonális transzformációt.
3. Deriváló operáció. Legyen V a legfeljebb másodfokú polinomfüggvények tere. Ekkor a
lineáris leképezés:
Bázis V-ben: {1, x, x2}, ezért a mátrixa:
Világos, hogy a leképezés képzere nem a teljes V, hanem annak egy altere (a legfeljebb elsőfokú polinomfüggvények tere) és nem csak a 0 polinom képe 0, hanem minden konstans polinomé.
Képtér, magtér
A magtere:
Ez tényleg altér, mert ha v, u ∈ Ker(A), akkor A v=A u = 0 és
A magtér az A injektivitásával van kapcsolatban. A injektív, ha
Azaz minden v - u alakú vektorra:
de minden vektor v - u alakú, ezért ez pontosan azt jelenti, hogy Ker(A)={0} a triviális altér.
A képtere:
Ez szintén altér, mert ha vesszük két képtérbeli elem lineáris kombinációját, akkor szintén valamilyen elem képe.
Ez a szűrjektivitással van kapcsolatban. A szűrjektív, ha
márpedig Im(A)=V2 pontosan azt jelenti, hogy az érkezési halmaz minden vektora előáll képként.
A két altér dimenziója között szoros kapcsolat van:
Dimenziótétel. Ha A : V1  V2 véges dimenziós terek között ható lineáris leképezés, akkor
V2 véges dimenziós terek között ható lineáris leképezés, akkor
Bizonyítás. Azt kell belátnunk, hogy Ker(A) egy bázisának száma + Im(A) egy bázisának száma = V1 egy bázisának száma. Legyen dim V1 = n és dim Ker(A) = k. Rögzítsük Ker(A) egy
bázisát. Világos, hogy dim A(<B>) = {0}, ezért a képtér nemnulla pontjaiba csak úgy juthatunk, ha <B>-n kívüli elemet választunk -- válasszunk annyit, mely az egész V1-et generálja, egészítsük ki B-t a V1 egy bázisává a C halmaz hozzávételével:
Ezek speciális tulajdonsága, hogy
azaz közösen kifeszítik a V1-et és a kifeszített alterek közös része a {0}. Ugyanis, ha v ∈ <B>∩<C>, akkor
és
akkor ezeket kivonva:
Amiből a BUC függetlensége miatt következik:
- 0 = λ1 = λ2 = ... = λk = μ1 = μ2 = ... = μl
Ekkor a D={ Ac1, Ac2, ...,Acl } vektorrendszer bázisa lesz Im(A)-nak. Ugyanis
1. D kifeszíti Im(A)-t. Egy
elemmel:
2. D lineárisan független. Ha ugyanis
akkor
azaz
Főtengelytétel
Az Rn  Rn leképezést szimmetrikusnak nevezünk, ha a szenderd bázisban szimmetrikus a mátrixa. Ekkor minden ortonormált bázisban is szimmetrikus lesz a mártixa. Ezek között a bázisok között az átváltó mátrix ortogonális, azaz
Rn leképezést szimmetrikusnak nevezünk, ha a szenderd bázisban szimmetrikus a mátrixa. Ekkor minden ortonormált bázisban is szimmetrikus lesz a mártixa. Ezek között a bázisok között az átváltó mátrix ortogonális, azaz
Értelmezhető leképezés transzponáltja is, mert ortnormált bázisok közötti átváltás invariáns a transzponálásra. Általában az átváltott mátrix:
alakú. Ortogonális transzformáció esetén pedig
Ekkor a szimmetria pont azt jelenti, hogy A=AT.
Főtengelytétel. Szimmetrikus leképezés sajátvektoraiból ortonormált bázis alkotható csupa valós sajátértékekkel.
Lineáris leképezések folytonossága
Megjegyzés. A normált terek között ható A lineáris leképezés folytonos, ha a 0-ban folytonos.
Ugyanis, legyen az A: N1  N2 lineáris leképezés és tegyük fel, hogy 0-ban folytonos, azaz minden ε>0-ra létezik δ>0, hogy minden x ∈ Bδ(0)-ra Ax ∈ Bε(0).
N2 lineáris leképezés és tegyük fel, hogy 0-ban folytonos, azaz minden ε>0-ra létezik δ>0, hogy minden x ∈ Bδ(0)-ra Ax ∈ Bε(0).
Most ha ε > 0 tetszőleges és x1 és x2 N1-beliek is tetszőlegesek, akkor
amennyiben x1-x2 ∈ Bδ(0), ahol δ a 0-beli folytonosság által az ε-hoz tartozó δ.
Tétel. A : Rn  Rm lineáris leképzés folytonos, sőt:
Rm lineáris leképzés folytonos, sőt:
Megjegyzés. Ez azt is jelenti, hogy egy ilyen leképezés Lipschitz-függvény. Az f: Rn ⊃ Rm függvényt Lipschitz-függvénynek nevezük, ha létezik L nemnegatív szám, hogy minden x1 és x2 Dom(f)-belire:
Rm függvényt Lipschitz-függvénynek nevezük, ha létezik L nemnegatív szám, hogy minden x1 és x2 Dom(f)-belire:
Világos, hogy ez lineáris leképezésre ekvivalens a tételbeli megfogalmazással.
Ha lipschitzes, akkor pedig folytonos, mert ekkor δ=ε/(L+1)-gyel
Bizonyítás. Vegyük az A sztenderd bázis beli mátrixát. Ekkor A(x)=A x. Így A minden Ai sorára
x. Így A minden Ai sorára
ahol Li rögzített i mellett a {|Ai,j|} j=1...n számok maximuma. Ha most vesszük L = max {Li}-t is, akkor
is teljesül, azaz a kép maximumnormája felülbecsülhető L-szer a vektor norma-1 szerinti normájával. A normák ekvivalenciája miat pedig alkalmas L-re minden normára igaz.
Operátornorma
A lineáris leképezések Lin(Rn,Rm) tere normált tér, ugyanis vegyük a következő számot:
Ez létezik, mivel x  ||Ax|| folytonos a kompakt 0 középpontú, egységsugarú gömbfelületen.
||Ax|| folytonos a kompakt 0 középpontú, egységsugarú gömbfelületen.
Differenciálhatóság
A többváltozós differenciálhatóságot az egyváltozós alábbi átfogalmazásából általánosítjuk:
Definíció. Legyen f: Rn  Rm és u ∈ int Dom(f). Azt mondjuk, hogy f differenciálható az u pontban, ha létezik olyan A: Rn
Rm és u ∈ int Dom(f). Azt mondjuk, hogy f differenciálható az u pontban, ha létezik olyan A: Rn  Rm lineáris leképezés, hogy
Rm lineáris leképezés, hogy
Ekkor A egyértelmű és az f leképezés u-bent beli differenciáljának nevezzük és df(u)-val vagy Df(u)-val jelöljük. Ezt a fogalmat néha teljes differenciálnak, totális differenciálnak vagy Fréchet-deriváltnak is mondjuk.
Megjegyzés. A fenti határérték 0 volta egyenértékű a következő kijelentéssel. Létezik A: Rn  Rm lineáris leképezés és ε: Dom(f)
Rm lineáris leképezés és ε: Dom(f)  Rm függvény, melyre:
Rm függvény, melyre:
- ε folytonos u-ban és ε(u)=0, továbbá
minden x ∈ Dom(f)-re:
Megjegyzés. Azt, hogy A egyértelmű, a következőkkel bizonyíthatjuk. Legyen A és B is a mondott tulajdonságú, azaz létezzenek ε és η az u-ban eltűnő és ott folytonos Dom(f)-en értelmezett függvények, melyekre teljesül, hogy minden x ∈ Dom(f)-re
ezeket kivonva egymásból és használva minden x-re:
így minden x = u + ty értékre is az azonosan nullát kapjuk, ha t pozitív szám, y pedig rögzített nemnulla vektor, azaz minden t-re
az azonosan 0 függény határértéke t 0 esetén szintén nulla:
0 esetén szintén nulla:
hiszen t-t kiemelhetünk és egyszerűsíthetünk és t 0 esetén
ε és η nullává válik.
Ez viszont pont azt jelenti, hogy a két lineéris operátor azonosan egyenlő.
0 esetén
ε és η nullává válik.
Ez viszont pont azt jelenti, hogy a két lineéris operátor azonosan egyenlő.
Jacobi-mátrix
A df(u) lineáris leképezés (e1,e2,...,en) szetenderd bázisbeli mátrixa legyen: [df(u)] = A. Vizsgáljuk mibe viszi a bázisokat df(u) leképezés!
Írjuk fel a definíciót, de az e1 egységvektor mentén tartsunk u-hoz: x = u + te1. Ekkor
ami azért hasznos, mert a
alakból kiemelhetó t:
azaz
vagyis f koordinátafüggvényeinek az első változó szerinti parciális deriváltja az u pontban. A többi oszlopvektor ugyanígy:
amelyet Jacobi-mátrixnak nevezünk.
Következmény. Tehát. ha f totálisan differenciálható, akkor parciálisan is differenciálható és a differenciál sztenderd bázisbeli mátrixa a Jacobi-mátrix.
Azaz:
- teljes differenciálhatóság
 parciális differenciálhatóság
parciális differenciálhatóság
de ez fordítva már nem igaz:
- parciális differenciálhatóság
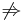 teljes differenciálhatóság
teljes differenciálhatóság
Erre vonatkozik a két alábbi példa.
| pótló gyakorlat | 5. gyakorlat |

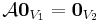
![[\mathcal{A}]_{B,C} = \begin{bmatrix}
\begin{matrix}\vert \\ \vert \\ \mathcal{A}\mathbf{b}_1 \\ \vert \\ \vert \end{matrix}& \begin{matrix}\vert \\ \vert \\ \mathcal{A}\mathbf{b}_2 \\ \vert \\ \vert \end{matrix} & ... & \begin{matrix}\vert \\ \vert \\ \mathcal{A}\mathbf{b}_n \\ \vert \\ \vert \end{matrix}
\end{bmatrix}](/upload/math/e/2/1/e218d5327c820937af47e217f5212ec7.png)
![[\mathcal{F}_\varphi]=\begin{bmatrix}\cos\varphi & -\sin\varphi \\ \sin\varphi & \cos\varphi \end{bmatrix}](/upload/math/1/b/d/1bd899a86970ed93aad1b307d1af4e0b.png)
![[\mathcal{T}_\varphi]=\begin{bmatrix}\cos(2\varphi) & \sin(2\varphi) \\ \sin(2\varphi) & -\cos(2\varphi) \end{bmatrix}](/upload/math/4/f/3/4f3d3c1c23cacad098bf0349140e0d0f.png)
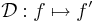
![[\mathcal{D}]=
\begin{bmatrix}
0 & 1 & 0 \\
0 & 0 & 2\\
0 & 0 & 0
\end{bmatrix}](/upload/math/a/7/a/a7ad5c2aa1f95e6c92807ec3550700c1.png)
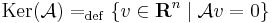
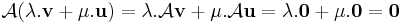
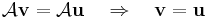
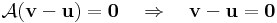
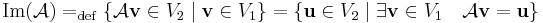

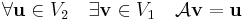
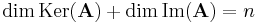
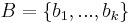
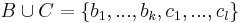
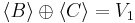
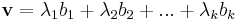
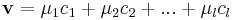
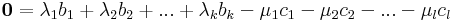
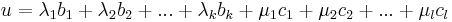
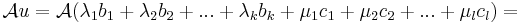
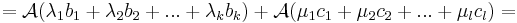
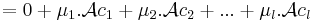
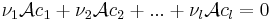
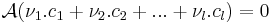
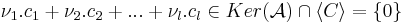
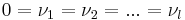
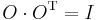
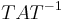
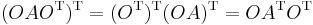
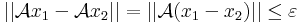
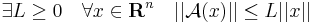
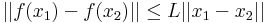
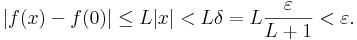
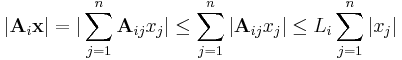
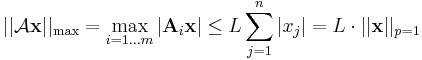
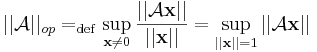
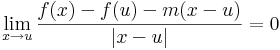

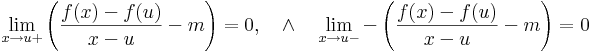
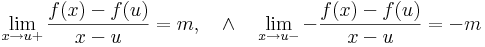
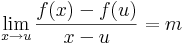
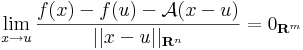
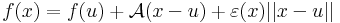
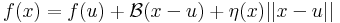
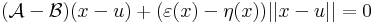
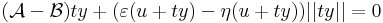
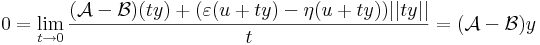
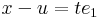
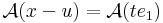
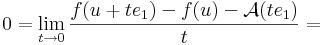
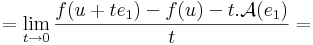
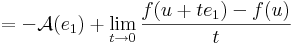
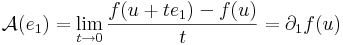
![[\mathrm{d}f(u)]=\mathbf{J}^f(u)=\begin{bmatrix}
\partial_1 f_1(u) & \partial_2 f_1(u) & \dots & \partial_n f_1(u)\\
\partial_1 f_2(u) & \partial_2 f_2(u) & \dots & \partial_n f_2(u)\\
\vdots & \vdots & \ddots & \vdots \\
\partial_1 f_m(u) & \partial_2 f_m(u) & \dots & \partial_n f_m(u)\\
\end{bmatrix}](/upload/math/b/c/8/bc8c1cf3c3d6f5032a7858552cc82a3a.png)