|
|
| 40. sor: |
40. sor: |
| | :<math>[\mathcal{A}(e_1)]=[\partial_1(\partial_1 f)(u)\quad \partial_1(\partial_2 f)(u)]=[\partial_{11} f(u)\quad \partial_{12}f(u)]</math> | | :<math>[\mathcal{A}(e_1)]=[\partial_1(\partial_1 f)(u)\quad \partial_1(\partial_2 f)(u)]=[\partial_{11} f(u)\quad \partial_{12}f(u)]</math> |
| | Az 1 bázisvektoron felvett érték tehát az a lineáris operártor, melyet a fenti sorvektorral való szorzás határoz meg. A másik bázisvektoron szintén felríható ez a mátrix, így világos, hogy d(df(.))(u) jellemezhető a d<sup>2</sup>f(u) mátrixával, így azonosítható vele. | | Az 1 bázisvektoron felvett érték tehát az a lineáris operártor, melyet a fenti sorvektorral való szorzás határoz meg. A másik bázisvektoron szintén felríható ez a mátrix, így világos, hogy d(df(.))(u) jellemezhető a d<sup>2</sup>f(u) mátrixával, így azonosítható vele. |
| − | ==Többváltozós függvény szélsőértéke==
| |
| − | ===Szélsőérték szükséges feltétele===
| |
| − | '''Tétel''' - ''Fermat-tétel'' - Legyen ''f'': '''R'''<sup>n</sup> <math>\supset\!\to</math> '''R''', ''u'' ∈ int Dom(''f''), ''f'' differenciálható ''u''-ban.
| |
| − | :Ha ''u''-ban ''f''-nek (lokális) szélsőértéke van, akkor
| |
| − | ::<math>\mathrm{grad}\,f(u)=0_{\mathbf{R}^n}\,</math>
| |
| − | ''U.is:'' minden ''i''-re az ''i''-edik parciális függvénynek szélsőértéke van ''u''<sub>i</sub>-ben, így az egyváltozós Fermat-tétel miatt ezeknek a deriváltja ''u''<sub>i</sub>-ben 0, így a gradiens értéke 0.
| |
| − |
| |
| − | ====Példa====
| |
| − | :<math>f(x,y)=x^2y^2\,</math>
| |
| − | Ennek gradiense:
| |
| − | :<math>\mathrm{grad}\,f(x,y)=(2xy^2,2yx^2)</math>
| |
| − | Az
| |
| − | :<math>\left.
| |
| − | \begin{matrix}
| |
| − | \mathrm{I.} & 2xy^2 & = & 0\\
| |
| − | \mathrm{II.} & 2yx^2 & = & 0\\
| |
| − | \end{matrix}
| |
| − | \right\}</math>
| |
| − | egyenletrendszer megoldásai: ''x'' = 0, ''y'' tetszőleges ill. ''y'' = 0 és ''x'' tetszőleges. A szélsőértékek helyei csak ezek közül kerülhetnek ki és ezek valóban szélsőértékek is, mert ezeken a függvény 0-t vesz fel, ami a lehetséges legkisebb értéke.
| |
| − | :<gnuplot>
| |
| − | set pm3d
| |
| − | set size 0.8,0.8
| |
| − | set xrange [-1:1]
| |
| − | set yrange [-1:1]
| |
| − | set zrange [-2:2]
| |
| − | set view 50,30,1,1
| |
| − | unset xtics
| |
| − | unset ytics
| |
| − | unset ztics
| |
| − | unset key
| |
| − | unset colorbox
| |
| − | splot 5*x*x*y*y
| |
| − | </gnuplot>
| |
| − | ===Másodikderivált próba===
| |
| − | Kétszer differenciálható függvényre vonatkozóan megfogalmazhatjuk a lokális maximum és minimum létezésének elégséges feltételét. Csak a kétváltozós függvényekkel foglalkozunk. Tegyük fel, hogy grad ''f''(u) = 0 és H<sup>f</sup>(u) az ''f'' Hesse-mátrixa
| |
| − | # ha det H<sup>f</sup>(u) > 0 és ∂<sub>11</sub>''f''(''u'') < 0, akkor ''f''-nek ''u''-ban '''maximuma''' van
| |
| − | # ha det H<sup>f</sup>(u) > 0 és ∂<sub>11</sub>''f''(''u'') > 0, akkor ''f''-nek ''u''-ban '''minimuma''' van
| |
| − | # ha det H<sup>f</sup>(u) < 0, akkor ''f''-nek biztosan nincs szélsőértéke, ún. '''nyeregpont'''ja van
| |
| − | # ha det H<sup>f</sup>(u) = 0, akkor a próba nem járt sikerrel, azaz további vizsgálatokat igényel annak eldöntése, hogy ''u'' szélsőérték hely-e.
| |
| − |
| |
| − | ''Megjegyzések.'' Mivel kétváltozós esetben
| |
| − | :<math>\mathrm{det}\,\mathrm{H}^f(u)=\partial_{11}f(u)\cdot \partial_{22}f(u)-(\partial_{12}f(u))^2</math>
| |
| − | ezért olyan eset nem létezik, hogy det H<sup>f</sup>(u) > 0 és ∂<sub>11</sub>''f''(''u'') = 0.
| |
| − |
| |
| − | Világos, hogy a másodikderivált tipikusan azoknál a függvényeknél jár sikerrel, melyeket egy másodfokú függvény közelít a legjobban (aszimptotikusan másodfokúak). Ha a függvény ennél magasabb fokú, akkor a második deriváltak eltűnnek és a Hesse-mártix elfajul (vagy legalább is tipikusan elfajul).
| |
| − |
| |
| − | Ha tehát
| |
| − | :<math>\mathrm{H}^{f}(u)=\begin{pmatrix}
| |
| − | A & B \\
| |
| − | B & C
| |
| − | \end{pmatrix}</math>, akkor <math>\mathrm{det\,H}^{f}(u)=AC - B^2 </math>,
| |
| − | és így a tipikus példák a következők.
| |
| − |
| |
| − | ====Példák====
| |
| − |
| |
| − | '''1.''' Ha B kicsi, azaz az AC-hez képest kis abszolútrétékű szám, akkor a szélsőérték irányába mozdul el a feladat.
| |
| − | :<math>f(x,y)=x^2+xy+y^2\,</math>
| |
| − |
| |
| − | Ekkor grad ''f'' = ( 2x + y , 2y + x ) és
| |
| − | :<math>\mathrm{H}^{f}(x,y)=\begin{pmatrix}
| |
| − | 2 & 1 \\
| |
| − | 1 & 2
| |
| − | \end{pmatrix}</math>
| |
| − | azaz 4 - 1 = 3 > 0 és 2 > 0 miatt minimum.
| |
| − | :<gnuplot>
| |
| − | set pm3d
| |
| − | set size 0.8,0.8
| |
| − | set xrange [-1:1]
| |
| − | set yrange [-1:1]
| |
| − | set zrange [-2:2]
| |
| − | set view 50,30,1,1
| |
| − | unset xtics
| |
| − | unset ytics
| |
| − | unset ztics
| |
| − | unset key
| |
| − | unset colorbox
| |
| − | splot x*x+x*y+y*y
| |
| − | </gnuplot>
| |
| − |
| |
| − | '''2.''' Ha |B| nagy (azaz AC-hez képest nagy), akkor a bizonyosan nemszélsőérték irányába.
| |
| − | :<math>f(x,y)=x^2-3xy+y^2\,</math>
| |
| − |
| |
| − | Ekkor grad ''f'' = ( 2x + -3y , 2y + -3x ) és
| |
| − | :<math>\mathrm{H}^{f}(x,y)=\begin{pmatrix}
| |
| − | 2 & -3 \\
| |
| − | -3 & 2
| |
| − | \end{pmatrix}</math>
| |
| − | azaz 4 - 9 = -5 < 0 miatt nincs szélsőérték: nyeregpont.
| |
| − | :<gnuplot>
| |
| − | set pm3d
| |
| − | set size 0.8,0.8
| |
| − | set xrange [-1:1]
| |
| − | set yrange [-1:1]
| |
| − | set zrange [-2:2]
| |
| − | set view 50,30,1,1
| |
| − | unset xtics
| |
| − | unset ytics
| |
| − | unset ztics
| |
| − | unset key
| |
| − | unset colorbox
| |
| − | splot x*x -3*x*y+y*y
| |
| − | </gnuplot>
| |
| − |
| |
| − | '''3.''' Negatív A és C-re és kis B-re:
| |
| − | :<math>f(x,y)=-x^2+xy-y^2\,</math>
| |
| − |
| |
| − | Ekkor grad ''f'' = ( -2x + 3y , -2y + 3x ) és
| |
| − | :<math>\mathrm{H}^{f}(x,y)=\begin{pmatrix}
| |
| − | -2 & 1 \\
| |
| − | 1 & -2
| |
| − | \end{pmatrix}</math>
| |
| − | azaz 4 - 1 = 3 > 0 és -2 < 0 miatt maximum.
| |
| − | :<gnuplot>
| |
| − | set pm3d
| |
| − | set size 0.8,0.8
| |
| − | set xrange [-1:1]
| |
| − | set yrange [-1:1]
| |
| − | set zrange [-2:2]
| |
| − | set view 50,30,1,1
| |
| − | unset xtics
| |
| − | unset ytics
| |
| − | unset ztics
| |
| − | unset key
| |
| − | unset colorbox
| |
| − | splot -x*x +x*y-y*y
| |
| − | </gnuplot>
| |
| − |
| |
| − | '''4.''' Ha A és C előjele ellenkező, akkor rögtön következik, hogy nincs sz.é.
| |
| − | :<math>f(x,y)=x^2+xy-y^2\,</math>
| |
| − |
| |
| − | Ekkor grad ''f'' = ( 2x + y , -2y + x ) és
| |
| − | :<math>\mathrm{H}^{f}(x,y)=\begin{pmatrix}
| |
| − | 2 & 1 \\
| |
| − | 1 & -2
| |
| − | \end{pmatrix}</math>
| |
| − | azaz -4 - 1 = -5 < 0 azaz nyeregpont.
| |
| − | :<gnuplot>
| |
| − | set pm3d
| |
| − | set size 0.8,0.8
| |
| − | set xrange [-1:1]
| |
| − | set yrange [-1:1]
| |
| − | set zrange [-2:2]
| |
| − | set view 50,30,1,1
| |
| − | unset xtics
| |
| − | unset ytics
| |
| − | unset ztics
| |
| − | unset key
| |
| − | unset colorbox
| |
| − | splot x*x +x*y-y*y
| |
| − | </gnuplot>
| |
| − |
| |
| − | '''5.''' Atipikus eset, ha AC = B<sup>2</sup>. Ekkor nem jár sikerrel a próba:
| |
| − | :<math>f(x,y)=x^2+2xy+y^2\,</math>
| |
| − |
| |
| − | Ekkor grad ''f'' = ( 2x + 2y , 2y + 2x ) és
| |
| − | :<math>\mathrm{H}^{f}(x,y)=\begin{pmatrix}
| |
| − | 2 & 2 \\
| |
| − | 2 & 2
| |
| − | \end{pmatrix}</math>
| |
| − | azaz 4 - 4 = 0, azaz határozatlan eset.
| |
| − | De tudjuk, hogy
| |
| − | :<math>f(x,y)=(x+y)^2\,</math>
| |
| − | ami pontosan akkor minimális, ha x = -y, azaz ezeken a helyeken van szélsőérték.
| |
| − | :<gnuplot>
| |
| − | set pm3d
| |
| − | set size 0.8,0.8
| |
| − | set xrange [-1:1]
| |
| − | set yrange [-1:1]
| |
| − | set zrange [-2:2]
| |
| − | set view 50,30,1,1
| |
| − | unset xtics
| |
| − | unset ytics
| |
| − | unset ztics
| |
| − | unset key
| |
| − | unset colorbox
| |
| − | splot (x+y)*(x+y)
| |
| − | </gnuplot>
| |
| | | | |
| | | | |
Ennek Jacobi-mátrixa akkor is létezik, ha csak azt feltételezzük, hogy a parciális deriváltak léteznek az u egykörnyezetében, és ott differenciálhatóak. Ekkor a szóban forgó Jacobi-mátrix kvadratikus és
(A tétel egy gyenge verziójának könnyen átlátható szemléletes bizonyítása megtalálható itt: User:Mozo/egyéb#Young-tétel.)
Általában a deriváltmátrixok nem szimmetrikusak, ez egy különleges tulajdonsága a második differenciálnak. Sőt, általában az a kérdés, hogy mi a deriválttenzor szimmetrikus és antiszimmetrikus része.
ami a kivonás és az osztást komponensenként elvégezve az parciális deriváltak első változó szerinti parciális deriváltjait adja:
Az 1 bázisvektoron felvett érték tehát az a lineáris operártor, melyet a fenti sorvektorral való szorzás határoz meg. A másik bázisvektoron szintén felríható ez a mátrix, így világos, hogy d(df(.))(u) jellemezhető a d2f(u) mátrixával, így azonosítható vele.
R lináris leképezések terébe képez (az ún. kétváltozós lineáris funkcionálok terébe). Ebben a norma az operátornorma (az operátor minimális Lipschitz-konstansa), és a tér véges dimenziós. A differenciálhatóság pontosan ugyanúgy értelmezhető, mint a többváltozs esetben. Ekkor az f függvény u-beli másodrendű differenciálja az
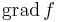
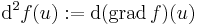
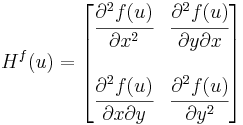
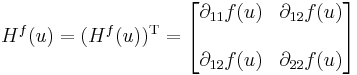
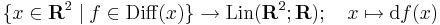
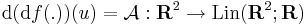
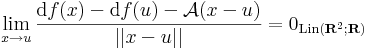
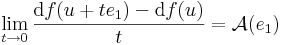
![\lim\limits_{t\to 0}\frac{[\partial_1 f(u+te_1)\quad\partial_2 f(u+te_1)]-[\partial_1 f(u)\quad\partial_2 f(u)]}{t}=[\mathcal{A}(e_1)]](/upload/math/4/3/4/4348717f73929046f534636df3b69051.png)
![[\mathcal{A}(e_1)]=[\partial_1(\partial_1 f)(u)\quad \partial_1(\partial_2 f)(u)]=[\partial_{11} f(u)\quad \partial_{12}f(u)]](/upload/math/2/5/3/2532edd298a88bdb9dfb65aa08cac917.png)
