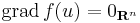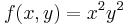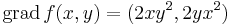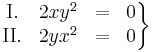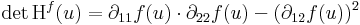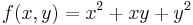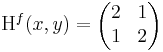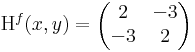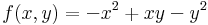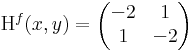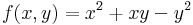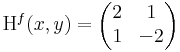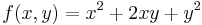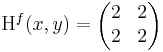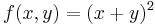Matematika A2a 2008/7. gyakorlat
- Ez az szócikk a Matematika A2a 2008 alszócikke.
Tartalomjegyzék |
Másodrendű parciális deriváltak
Ha f a H ⊆ R2 halmazon értelmezett R-be képező, az u ∈ H-ban differenciálható függvény és a
gradiensfüggvény szintén differenciálható u-ban, akkor f-et u-ban kétszer differenciálhatónak nevezzük és az f függény u-beli másodrendű differenciálja:
Ennek Jacobi-mátrixa akkor is létezik, ha csak azt feltételezzük, hogy a parciális deriváltak léteznek az u egykörnyezetében, és ott differenciálhatóak. Ekkor a szóban forgó Jacobi-mátrix kvadratikus és
alakú, amit Hesse-féle mátrixnak nevezünk.
A vegyes másodrendű parciális deriváltakra vonatkozik a Young-tétel:
Tétel (Young) Kétszer differenciálható függvény vegyes másodrendű parciális deriváltjai egyenlők.
(A tétel egy gyenge verziójának könnyen átlátható szemléletes bizonyítása megtalálható itt: User:Mozo/egyéb#Young-tétel.)
A Young-tétel értelmében a Hesse-mátrix szimmetrikus illetve a d2f(u) szimmetrikus tenzor
Általában a deriváltmátrixok nem szimmetrikusak, ez egy különleges tulajdonsága a második differenciálnak. Sőt, általában az a kérdés, hogy mi a deriválttenzor szimmetrikus és antiszimmetrikus része.
Megjegyzés. Elvileg a
leképezésnek kellett volna a differenciálját venni az u pontban, és ezt tekinteni a differenciálnak. Ám ez nem Rm-be, hanem egy általánosabb normált térbe, a R2  R lináris leképezések terébe képez (az ún. kétváltozós lineáris funkcionálok terébe). Ebben a norma az operátornorma (az operátor minimális Lipschitz-konstansa), és a tér véges dimenziós. A differenciálhatóság pontosan ugyanúgy értelmezhető, mint a többváltozs esetben. Ekkor az f függvény u-beli másodrendű differenciálja az
R lináris leképezések terébe képez (az ún. kétváltozós lineáris funkcionálok terébe). Ebben a norma az operátornorma (az operátor minimális Lipschitz-konstansa), és a tér véges dimenziós. A differenciálhatóság pontosan ugyanúgy értelmezhető, mint a többváltozs esetben. Ekkor az f függvény u-beli másodrendű differenciálja az
lineáris leképezés, melyre teljesül a
A bázisvektorokon A a következőt veszi fel:
ennek a mátrixa a sztenderd bázisban
ami a kivonás és az osztást komponensenként elvégezve az parciális deriváltak első változó szerinti parciális deriváltjait adja:
Az 1 bázisvektoron felvett érték tehát az a lineáris operártor, melyet a fenti sorvektorral való szorzás határoz meg. A másik bázisvektoron szintén felríható ez a mátrix, így világos, hogy d(df(.))(u) jellemezhető a d2f(u) mátrixával, így azonosítható vele.
Többváltozós függvény szélsőértéke
Szélsőérték szükséges feltétele
Tétel - Fermat-tétel - Legyen f: Rn 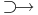 R, u ∈ int Dom(f), f differenciálható u-ban.
R, u ∈ int Dom(f), f differenciálható u-ban.
- Ha u-ban f-nek (lokális) szélsőértéke van, akkor
U.is: minden i-re az i-edik parciális függvénynek szélsőértéke van ui-ben, így az egyváltozós Fermat-tétel miatt ezeknek a deriváltja ui-ben 0, így a gradiens értéke 0.
Példa
Ennek gradiense:
Az
egyenletrendszer megoldásai: x = 0, y tetszőleges ill. y = 0 és x tetszőleges. A szélsőértékek helyei csak ezek közül kerülhetnek ki és ezek valóban szélsőértékek is, mert ezeken a függvény 0-t vesz fel, ami a lehetséges legkisebb értéke.
set pm3d
set size 0.8,0.8 set xrange [-1:1] set yrange [-1:1] set zrange [-2:2] set view 50,30,1,1 unset xtics unset ytics unset ztics unset key unset colorboxsplot 5*x*x*y*y
Másodikderivált próba
Kétszer differenciálható függvényre vonatkozóan megfogalmazhatjuk a lokális maximum és minimum létezésének elégséges feltételét. Csak a kétváltozós függvényekkel foglalkozunk. Tegyük fel, hogy grad f(u) = 0 és Hf(u) az f Hesse-mátrixa
- ha det Hf(u) > 0 és ∂11f(u) < 0, akkor f-nek u-ban maximuma van
- ha det Hf(u) > 0 és ∂11f(u) > 0, akkor f-nek u-ban minimuma van
- ha det Hf(u) < 0, akkor f-nek biztosan nincs szélsőértéke, ún. nyeregpontja van
- ha det Hf(u) = 0, akkor a próba nem járt sikerrel, azaz további vizsgálatokat igényel annak eldöntése, hogy u szélsőérték hely-e.
Megjegyzések. Mivel kétváltozós esetben
ezért olyan eset nem létezik, hogy det Hf(u) > 0 és ∂11f(u) = 0.
Világos, hogy a másodikderivált tipikusan azoknál a függvényeknél jár sikerrel, melyeket egy másodfokú függvény közelít a legjobban (aszimptotikusan másodfokúak). Ha a függvény ennél magasabb fokú, akkor a második deriváltak eltűnnek és a Hesse-mártix elfajul (vagy legalább is tipikusan elfajul).
Ha tehát
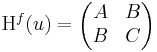 , akkor
, akkor 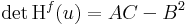 ,
,
és így a tipikus példák a következők.
Példák
1. Ha B kicsi, azaz az AC-hez képest kis abszolútrétékű szám, akkor a szélsőérték irányába mozdul el a feladat.
Ekkor grad f = ( 2x + y , 2y + x ) és
azaz 4 - 1 = 3 > 0 és 2 > 0 miatt minimum.
set pm3d
set size 0.8,0.8 set xrange [-1:1] set yrange [-1:1] set zrange [-2:2] set view 50,30,1,1 unset xtics unset ytics unset ztics unset key unset colorboxsplot x*x+x*y+y*y
2. Ha |B| nagy (azaz AC-hez képest nagy), akkor a bizonyosan nemszélsőérték irányába.
Ekkor grad f = ( 2x + -3y , 2y + -3x ) és
azaz 4 - 9 = -5 < 0 miatt nincs szélsőérték: nyeregpont.
set pm3d
set size 0.8,0.8 set xrange [-1:1] set yrange [-1:1] set zrange [-2:2] set view 50,30,1,1 unset xtics unset ytics unset ztics unset key unset colorboxsplot x*x -3*x*y+y*y
3. Negatív A és C-re és kis B-re:
Ekkor grad f = ( -2x + 3y , -2y + 3x ) és
azaz 4 - 1 = 3 > 0 és -2 < 0 miatt maximum.
set pm3d
set size 0.8,0.8 set xrange [-1:1] set yrange [-1:1] set zrange [-2:2] set view 50,30,1,1 unset xtics unset ytics unset ztics unset key unset colorboxsplot -x*x +x*y-y*y
4. Ha A és C előjele ellenkező, akkor rögtön következik, hogy nincs sz.é.
Ekkor grad f = ( 2x + y , -2y + x ) és
azaz -4 - 1 = -5 < 0 azaz nyeregpont.
set pm3d
set size 0.8,0.8 set xrange [-1:1] set yrange [-1:1] set zrange [-2:2] set view 50,30,1,1 unset xtics unset ytics unset ztics unset key unset colorboxsplot x*x +x*y-y*y
5. Atipikus eset, ha AC = B2. Ekkor nem jár sikerrel a próba:
Ekkor grad f = ( 2x + 2y , 2y + 2x ) és
azaz 4 - 4 = 0, azaz határozatlan eset. De tudjuk, hogy
ami pontosan akkor minimális, ha x = -y, azaz ezeken a helyeken van szélsőérték.
set pm3d
set size 0.8,0.8 set xrange [-1:1] set yrange [-1:1] set zrange [-2:2] set view 50,30,1,1 unset xtics unset ytics unset ztics unset key unset colorboxsplot (x+y)*(x+y)
| 6. gyakorlat | 8. gyakorlat |
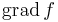
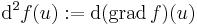
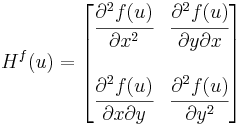
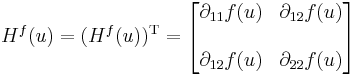
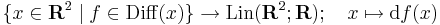
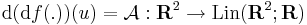
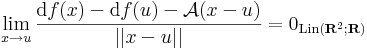
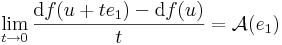
![\lim\limits_{t\to 0}\frac{[\partial_1 f(u+te_1)\quad\partial_2 f(u+te_1)]-[\partial_1 f(u)\quad\partial_2 f(u)]}{t}=[\mathcal{A}(e_1)]](/upload/math/4/3/4/4348717f73929046f534636df3b69051.png)
![[\mathcal{A}(e_1)]=[\partial_1(\partial_1 f)(u)\quad \partial_1(\partial_2 f)(u)]=[\partial_{11} f(u)\quad \partial_{12}f(u)]](/upload/math/2/5/3/2532edd298a88bdb9dfb65aa08cac917.png)