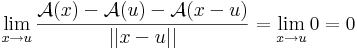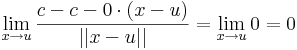Szerkesztő:Mozo/ A2 bizonyítások
Mozo (vitalap | szerkesztései) (→Weierstrass tétele) |
Mozo (vitalap | szerkesztései) (→Weierstrass tétele) |
||
| 62. sor: | 62. sor: | ||
:<math>h:K\to\mathbf{R};x\mapsto \frac{1}{S-f(x)}</math> | :<math>h:K\to\mathbf{R};x\mapsto \frac{1}{S-f(x)}</math> | ||
függvény. <math>h</math> mert folytonos függvényekből van folytonosságot megőrző módon összetéve. Az 1) pont szerint korlátos is, ami azonban ellentmond annak, hogy ''S'' a szuprémum. Ugyanis ''f'' minden határon túl megközelíti ''S''-et, azaz a különbségük reciproka minden határon túl nő. | függvény. <math>h</math> mert folytonos függvényekből van folytonosságot megőrző módon összetéve. Az 1) pont szerint korlátos is, ami azonban ellentmond annak, hogy ''S'' a szuprémum. Ugyanis ''f'' minden határon túl megközelíti ''S''-et, azaz a különbségük reciproka minden határon túl nő. | ||
| + | |||
| + | ==Differenciálhatóság== | ||
| + | ===Definíciója=== | ||
| + | Legyen ''f'': '''R'''<sup>n</sup> <math>\supset\!\longrightarrow</math> '''R'''<sup>m</sup> és ''u'' ∈ int Dom(f). Azt mondjuk, hogy ''f'' '''differenciálható''' az ''u'' pontban, ha létezik olyan ''A'': '''R'''<sup>n</sup> <math>\to</math> '''R'''<sup>m</sup> lineáris leképezés, hogy | ||
| + | :<math>\lim\limits_{x\to u}\frac{f(x)-f(u)-\mathcal{A}(x-u)}{||x-u||_{\mathbf{R}^n}}=0_{\mathbf{R}^m}</math> | ||
| + | Ekkor ''A'' egyértelmű és az ''f'' leképezés ''u''-bent beli '''deriválttenzor'''ának vagy '''differenciál'''jának nevezzük és d''f''(''u'')-val vagy D''f''(u)-val jelöljük. Ezt a fogalmat néha ''teljes differenciál''nak, ''totális differenciál''nak vagy ''Fréchet-derivált''nak is mondjuk. | ||
| + | ===Deriváltmátrix=== | ||
| + | Vizsgáljuk mibe viszi a bázisokat d''f''(''u'') komponensleképezésenként. A d''f''(''u'') lineáris leképezés (<math>e_1</math>,<math>e_2</math>,...,<math>e_n</math>) szetenderd bázisbeli mátrixa legyen: [d''f''(''u'')] = '''A'''. Világos, hogy (d''f''(''u''))(''x'')='''A''' ''x''. Először vegyük az '''A''' első sorvektorát, '''A'''<sub>1</sub>-et és az <math>e_1</math> egységvektor mentén tartunk ''u''-hoz: ''x'' = ''u'' + ''t''<math>e_1</math>. A d''f''(''u'')-t definiáló határértékegyenlőség ekkor a következő alakot ölti: | ||
| + | :<math>0=\lim\limits_{t\to 0}\frac{f_1(u+te_1)-f_1(u)-\mathbf{A}_1\cdot(te_1)}{t}=</math> | ||
| + | :::<math>=\lim\limits_{t\to 0}\frac{f_1(u+te_1)-f_1(u)-t\mathbf{A}_1\cdot(e_1)}{t}=</math> | ||
| + | :::<math>=-\mathbf{A}_1\cdot e_1+\lim\limits_{t\to 0}\frac{f_1(u+te_1)-f_1(u)}{t}</math> | ||
| + | azaz | ||
| + | :<math>\mathbf{A}_1\cdot e_1=\lim\limits_{t\to 0}\frac{f_1(u+te_1)-f_1(u)}{t}=\partial_1 f_1(u)</math> | ||
| + | vagyis ''f'' első koordinátafüggvényének <math>f_1</math>-nek az első változó szerinti parciális deriváltja az ''u'' pontban. A többi mátrixelemet ugyanígy: | ||
| + | |||
| + | :<math>[\mathrm{d}f(u)]=\mathbf{J}^f(u)=\begin{bmatrix} | ||
| + | \partial_1 f_1(u) & \partial_2 f_1(u) & \dots & \partial_n f_1(u)\\ | ||
| + | \partial_1 f_2(u) & \partial_2 f_2(u) & \dots & \partial_n f_2(u)\\ | ||
| + | \vdots & \vdots & \ddots & \vdots \\ | ||
| + | \partial_1 f_m(u) & \partial_2 f_m(u) & \dots & \partial_n f_m(u)\\ | ||
| + | \end{bmatrix}</math> | ||
| + | amelyet '''Jacobi-mátrix'''nak nevezünk. | ||
| + | |||
| + | ===Lineáris, konstans és affin függvény deriváltja=== | ||
| + | Az ''A'' : '''R'''<sup>n</sup> <math>\to</math> '''R'''<sup>m</sup> lineáris leképezés differenciálható és differenciálja minden pontban saját maga. | ||
| + | |||
| + | ''Ugyanis, '' legyen ''u'' ∈ '''R'''<sup>n</sup>. Ekkor | ||
| + | |||
| + | :<math>\lim\limits_{x\to u}\frac{\mathcal{A}(x)-\mathcal{A}(u)-\mathcal{A}(x-u)}{||x-u||}=\lim\limits_{x\to u}0=0</math> | ||
| + | |||
| + | c konstans függény esetén az d''c''(''u'') <math>\equiv</math> 0 alkalmas differenciálnak, mert | ||
| + | :<math>\lim\limits_{x\to u}\frac{c-c-0\cdot(x-u)}{||x-u||}=\lim\limits_{x\to u}0=0</math> | ||
| + | így világos, hogy c + ''A'' alakú affin függvények is differenciálhatóak, és differenciáljuk minden pontban az az ''A'' lineáris leképezés, melynek eltolásából az affin származik. Ezt szintén behelyettesítéssel ellenőrizhetjük. | ||
| + | |||
| + | Tehát minden ''u'' ∈ '''R'''<sup>n</sup>-re | ||
| + | :<math>\mathrm{d}\mathcal{A}(u)=\mathcal{A},\quad\quad\mathrm{d}c(u)\equiv 0,\quad\quad\mathrm{d}(b+\mathcal{A}\circ(id-a))(u)=\mathcal{A}</math> | ||
| + | |||
| + | ===Elégséges feltétel totális differenciálhatóságra=== | ||
| + | |||
| + | '''Tétel.''' Ha az ''f'':'''R'''<sup>n</sup> ⊃<math>\to</math> '''R'''<sup>m</sup> függvény minden parciális deriváltfüggvénye létezik az ''u'' egy környezetében és ''u''-ban a parciális deriváltak folytonosak, akkor ''u''-ban ''f'' differenciálható. | ||
A lap 2008. május 24., 07:56-kori változata
Tartalomjegyzék |
Többváltozós B–W-tétel
- Lásd még:Bolzano–Weierstrass-tétel
A többdimenziós (de nem végtelendimenziós) esetben a csúcselemes bizonyítás nem működik abban az értelmeben, hogy közvetlenül nem hivatkozhatunk rájuk, mert nincs RN-ben a műveletekkel kompatibilis rendezés. Gondolhatnók arra is, hogy komponensenként használjuk az egydimenziós B–W-tételt. Ezzel a következő a probléma. Világos, hogy létezik minden projekciósorozatra egy-egy részsorozat, mely konvergens. Ám ebből egyáltalán nem következtethetünk arra, hogy ezek metszetéből kiválasztható részsorozat. Ellenpéldaként vegyünk egy R2-ben haladó sorozatot. Tegyük fel, hogy (szerencsétlen módon) az egydimenziós B–W-tétel az első komponensek sorozatából a páros indexűeket, a második komponensek közül a páratéan indexűeket választja ki. Ekkor a kétdimenziós sorozatnak nincs olyan részsosozata, mely a komponensorozatok közös indexeikből válaszható ki, tekintve, hogy a közös indexen halmaza üres.
A fentiek miatt olyan módon kell konvergens részsorozatokat kiválasztanunk, mely bizonyosan végtelen sok közös indexel rendelkeznek. A konstrukció a következő.
Bizonyítás
Legyen
egy N komponensű sorozat, mely korlátos RN-ben. Ekkor a komponenssorozatok is korlátosak. Az egydimenziós B–W-tétel szerint az
sorozathoz létezik σ1 indexsorozat úgy, hogy az
konvergens részsorozat. Hasonlóképpen, de a
sorozatnak is van
konvergens részsorozata. Megállapíthatjuk, hogy a
sorozat szintén konvergens, mert konvergens sorozat részsorozata. Ugyanígy léteznek σ1, σ2, ..., σN indexsorozatok, hogy a
sorozatok mind konvergensek és így tetszőleges k=1...N-re
is az, ami pontosan azt jelenti, hogy az
sorozat komponensenként konvergens, azaz konvergens. A
tehát olyan indexsorozat, mely konvergens részsorozatot választ ki (an)-ből.
Ellenpélda végtelen dimenzióra
A tétel végtelen dimenziós esetben nem igaz. Vegyük példul a korlátos valós függvények
terében a szuprémumnormát:
és a belőle definiálható távolságot. Ebben az esetben a páratlan gyökkitevőjű gyökfüggvények
sorozata nem konvergens. Ez amiatt van, hogy az itteni konvergenciafogalom ugyanaz, mint a függvénysorozatok egyenletes konvergenciájának fogalma. Bár ez a függvénysorozat pontonként konvergál a szignumfüggvényhez, de a sorozat a szignumfüggvény minden környezetéből kilép. Emiatt még az is igaz, hogy egyetlen részsorozta sem lehet konvergens (azaz egyenletesen konvergens), holott a függvénysorozat maga korlátos (u.is. belefoglalható az azonosan 0 függvény 2 sugarú környezetébe).
Megjegyzés. A tétel azon iránya, mely a sorozatkompaktságot tételezi fel, igaz marad minden metrikus térben.
Weierstrass tétele
Az alábbiakban felhasználjuk a kompaktság fogalmát és Heine–Borel-tételt.
(Kompakt egy K halmaz, ha minden nyílt halmazrendszerből, melynek uniója lefedi K-t kiválasztható véges sok nyílt halmaz is, melyek véges uniója még mindig lefedi K-t.
Heine–Borel-tétel. Korlátos és zárt halmaz kompakt.)
Tétel (Weierstrass) Valós értékű, kompakt halmazon folytonos függvény felveszi minimumát és maximumát.
- (Ha f ∈ C(Rn,R), Dom(f) kompakt, akkor sup(f), inf(f) ∈ Ran(f) )
Bizonyítás.
1) Először belátjuk, hogy kompakt halmazon folytonos függvény korlátos. Legyen ugyanis ε tetszőleges pozitív szám és f értelmezési tartománya K. A folytonosság miatt K minden u eleméhez létezik δ(u) pozitív szám, hogy f a Bδ(u) környezeten belül mindvégig az (f(u)-ε,f(u)+ε) intervallumon belül mara. Ekkor nyílt halmazok {Bδ(u)(u) : u ∈ K} rendszere lefedi K-t, vagyis a Heine–Borel-tétel miatt már ebből véges sok is lefed. Legyen ez {Bδ(u)(u) : u ∈ F}, ahol tehát F ⊆ K véges. Ezek képei mind a (f(u)-ε,f(u)+ε) (u∈F)inervallumokban vannak, így a {(f(u)-ε,f(u)+ε) : u ∈ F} véges intervallumrendszer lefedi Ran(f)-et. Tehát f a "legmagasabb" intervallum felső határa és a "legalacsonyabb" intervallum alsó határa közé esik.
2) Belátjuk, hogy f felveszi a szuprémumát (és ugyanígy az infimumát is). Legyen S := sup(f) (azaz f értékkészletének legkisebb felső korlátja). Ekkor a g : K  R, x
R, x  S-f(x)függvény nemnegatív értékeket vesz föl. Ha f nem venné fel a szuprémumát, akkor g pozitív lenne. Ekkor értelmezhető lenne a
S-f(x)függvény nemnegatív értékeket vesz föl. Ha f nem venné fel a szuprémumát, akkor g pozitív lenne. Ekkor értelmezhető lenne a
függvény. h mert folytonos függvényekből van folytonosságot megőrző módon összetéve. Az 1) pont szerint korlátos is, ami azonban ellentmond annak, hogy S a szuprémum. Ugyanis f minden határon túl megközelíti S-et, azaz a különbségük reciproka minden határon túl nő.
Differenciálhatóság
Definíciója
Legyen f: Rn  Rm és u ∈ int Dom(f). Azt mondjuk, hogy f differenciálható az u pontban, ha létezik olyan A: Rn
Rm és u ∈ int Dom(f). Azt mondjuk, hogy f differenciálható az u pontban, ha létezik olyan A: Rn  Rm lineáris leképezés, hogy
Rm lineáris leképezés, hogy
Ekkor A egyértelmű és az f leképezés u-bent beli deriválttenzorának vagy differenciáljának nevezzük és df(u)-val vagy Df(u)-val jelöljük. Ezt a fogalmat néha teljes differenciálnak, totális differenciálnak vagy Fréchet-deriváltnak is mondjuk.
Deriváltmátrix
Vizsgáljuk mibe viszi a bázisokat df(u) komponensleképezésenként. A df(u) lineáris leképezés (e1,e2,...,en) szetenderd bázisbeli mátrixa legyen: [df(u)] = A. Világos, hogy (df(u))(x)=A x. Először vegyük az A első sorvektorát, A1-et és az e1 egységvektor mentén tartunk u-hoz: x = u + te1. A df(u)-t definiáló határértékegyenlőség ekkor a következő alakot ölti:
azaz
vagyis f első koordinátafüggvényének f1-nek az első változó szerinti parciális deriváltja az u pontban. A többi mátrixelemet ugyanígy:
amelyet Jacobi-mátrixnak nevezünk.
Lineáris, konstans és affin függvény deriváltja
Az A : Rn  Rm lineáris leképezés differenciálható és differenciálja minden pontban saját maga.
Rm lineáris leképezés differenciálható és differenciálja minden pontban saját maga.
Ugyanis, legyen u ∈ Rn. Ekkor
c konstans függény esetén az dc(u)  0 alkalmas differenciálnak, mert
0 alkalmas differenciálnak, mert
így világos, hogy c + A alakú affin függvények is differenciálhatóak, és differenciáljuk minden pontban az az A lineáris leképezés, melynek eltolásából az affin származik. Ezt szintén behelyettesítéssel ellenőrizhetjük.
Tehát minden u ∈ Rn-re
Elégséges feltétel totális differenciálhatóságra
Tétel. Ha az f:Rn ⊃ Rm függvény minden parciális deriváltfüggvénye létezik az u egy környezetében és u-ban a parciális deriváltak folytonosak, akkor u-ban f differenciálható.
Rm függvény minden parciális deriváltfüggvénye létezik az u egy környezetében és u-ban a parciális deriváltak folytonosak, akkor u-ban f differenciálható.
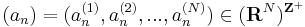
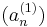
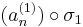
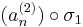
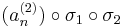
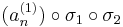

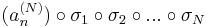
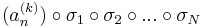
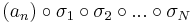
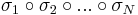
![\mathrm{B}([-1,+1],\mathbf{R})\,](/upload/math/6/f/8/6f81ef1e657e662d5f30dcfba319be40.png)
![||f||=_{\mathrm{def}}\sup\{|f(x)|\mid x\in [-1,+1]\}\,](/upload/math/9/e/c/9ec0abff769966a02d1869c5efc9881e.png)
![f_n=\sqrt[2n+1]{.\;}\quad\quad (f_n(x)=\sqrt[2n+1]{x})](/upload/math/6/8/1/68142b19ef9f58a8e151b2ea4973d681.png)
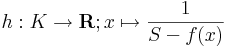
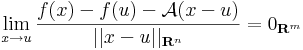
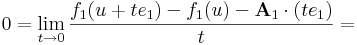
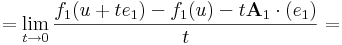
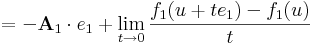
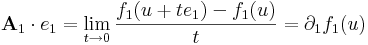
![[\mathrm{d}f(u)]=\mathbf{J}^f(u)=\begin{bmatrix}
\partial_1 f_1(u) & \partial_2 f_1(u) & \dots & \partial_n f_1(u)\\
\partial_1 f_2(u) & \partial_2 f_2(u) & \dots & \partial_n f_2(u)\\
\vdots & \vdots & \ddots & \vdots \\
\partial_1 f_m(u) & \partial_2 f_m(u) & \dots & \partial_n f_m(u)\\
\end{bmatrix}](/upload/math/b/c/8/bc8c1cf3c3d6f5032a7858552cc82a3a.png)