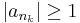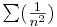Szerkesztő:Mozo/ A2 bizonyítások
Mozo (vitalap | szerkesztései) |
Mozo (vitalap | szerkesztései) (→Weierstrass tétele) |
||
| (egy szerkesztő 22 közbeeső változata nincs mutatva) | |||
| 1. sor: | 1. sor: | ||
| − | == | + | ==Többdimenziós Bolzano–Weierstrass-tétel== |
:''Lásd még:[[Bolzano–Weierstrass-tétel]]'' | :''Lásd még:[[Bolzano–Weierstrass-tétel]]'' | ||
A többdimenziós (de nem végtelendimenziós) esetben a csúcselemes bizonyítás nem működik abban az értelmeben, hogy közvetlenül nem hivatkozhatunk rájuk, mert nincs '''R'''<sup>N</sup>-ben a műveletekkel kompatibilis rendezés. Gondolhatnók arra is, hogy komponensenként használjuk az egydimenziós B–W-tételt. Ezzel a következő a probléma. Világos, hogy létezik minden projekciósorozatra egy-egy részsorozat, mely konvergens. Ám ebből egyáltalán nem következtethetünk arra, hogy ezek metszetéből kiválasztható részsorozat. Ellenpéldaként vegyünk egy '''R'''<sup>2</sup>-ben haladó sorozatot. Tegyük fel, hogy (szerencsétlen módon) az egydimenziós B–W-tétel az első komponensek sorozatából a páros indexűeket, a második komponensek közül a páratéan indexűeket választja ki. Ekkor a kétdimenziós sorozatnak nincs olyan részsosozata, mely a komponensorozatok ''közös'' indexeikből válaszható ki, tekintve, hogy a közös indexen halmaza üres. | A többdimenziós (de nem végtelendimenziós) esetben a csúcselemes bizonyítás nem működik abban az értelmeben, hogy közvetlenül nem hivatkozhatunk rájuk, mert nincs '''R'''<sup>N</sup>-ben a műveletekkel kompatibilis rendezés. Gondolhatnók arra is, hogy komponensenként használjuk az egydimenziós B–W-tételt. Ezzel a következő a probléma. Világos, hogy létezik minden projekciósorozatra egy-egy részsorozat, mely konvergens. Ám ebből egyáltalán nem következtethetünk arra, hogy ezek metszetéből kiválasztható részsorozat. Ellenpéldaként vegyünk egy '''R'''<sup>2</sup>-ben haladó sorozatot. Tegyük fel, hogy (szerencsétlen módon) az egydimenziós B–W-tétel az első komponensek sorozatából a páros indexűeket, a második komponensek közül a páratéan indexűeket választja ki. Ekkor a kétdimenziós sorozatnak nincs olyan részsosozata, mely a komponensorozatok ''közös'' indexeikből válaszható ki, tekintve, hogy a közös indexen halmaza üres. | ||
| 43. sor: | 43. sor: | ||
'''Megjegyzés. ''' A tétel azon iránya, mely a sorozatkompaktságot tételezi fel, igaz marad minden metrikus térben. | '''Megjegyzés. ''' A tétel azon iránya, mely a sorozatkompaktságot tételezi fel, igaz marad minden metrikus térben. | ||
| + | |||
| + | ==Weierstrass tétele== | ||
| + | |||
| + | Az alábbiakban felhasználjuk a kompaktság fogalmát (és esetleg a bizonyitas egy masik variansa a Heine–Borel-tételt). | ||
| + | |||
| + | (''Kompakt'' egy ''K'' halmaz, ha minden nyílt halmazrendszerből, melynek uniója lefedi ''K''-t kiválasztható véges sok nyílt halmaz is, melyek véges uniója még mindig lefedi ''K''-t. | ||
| + | |||
| + | ''Heine–Borel-tétel.'' Veges dimenzios normalt terben korlátos és zárt halmaz kompakt.) | ||
| + | |||
| + | '''Tétel''' (''Weierstrass'') Valós értékű, kompakt halmazon folytonos függvény felveszi minimumát és maximumát. | ||
| + | :(Ha ''f'' ∈ C('''R'''<sup>n</sup>,'''R'''), Dom(''f'') kompakt, akkor sup(''f''), inf(''f'') ∈ Ran(''f'') ) | ||
| + | |||
| + | ''Bizonyítás.'' | ||
| + | |||
| + | 1) Először belátjuk, hogy kompakt halmazon folytonos függvény korlátos. Legyen ugyanis ε tetszőleges pozitív szám és ''f'' értelmezési tartománya ''K''. A folytonosság miatt ''K'' minden ''u'' eleméhez létezik δ(''u'') pozitív szám, hogy ''f'' a B<sub>δ</sub>(''u'') környezeten belül mindvégig az (''f''(''u'')-ε,''f''(''u'')+ε) intervallumon belül marad. Ekkor a nyílt halmazokbol allo {B<sub>δ(u)</sub>(''u'') : ''u'' ∈ ''K''} rendszer lefedi ''K''-t, ami kompakt, azaz ebből mar véges sok is lefedi ''K''-t. Legyen ez {B<sub>δ(u)</sub>(''u'') : ''u'' ∈ ''F''}, ahol tehát ''F'' ⊆ ''K'' véges. Ezek képei mind a (''f''(''u'')-ε,''f''(''u'')+ε) (''u''∈''F'') intervallumokban vannak, így a {(''f''(''u'')-ε,''f''(''u'')+ε) : ''u'' ∈ ''F''} véges intervallumrendszer lefedi Ran(''f'')-et. Tehát ''f'' a "legmagasabb" intervallum felső határa és a "legalacsonyabb" intervallum alsó határa közé esik. | ||
| + | |||
| + | 2) Belátjuk, hogy ''f'' felveszi a szuprémumát (és ugyanígy az infimumát is). Legyen ''S'' := sup(''f'') (azaz ''f'' értékkészletének legkisebb felső korlátja). Ekkor a ''g'' : ''K'' <math>\to</math> '''R''', ''x'' <math>\mapsto</math> ''S''-''f''(''x'')függvény nemnegatív értékeket vesz föl. Ha ''f'' nem venné fel a szuprémumát, akkor ''g'' pozitív lenne. Ekkor értelmezhető lenne a | ||
| + | :<math>h:K\to\mathbf{R};x\mapsto \frac{1}{S-f(x)}</math> | ||
| + | függvény. <math>h</math> mert folytonos függvényekből van folytonosságot megőrző módon összetéve. Az 1) pont szerint korlátos is, ami azonban ellentmond annak, hogy ''S'' a szuprémum, mert ''f'' minden határon túl megközelíti ''S''-et. Ugyanis minden S - 1/''n'' számhoz létezik olyan <math>x_n</math> ∈ ''K'', hogy ''f''(<math>x_n</math>) > S - 1/''n''. Létezik tehát olyan (<math>x_n</math>) ''K''-ban haladó sorozat, melyre f(x_n) alulrúl az ''S''-hez tart. Ám, ekkor az 1/(S-f(<math>x_n</math>)) a +∞-hez tart, ami ''h'' korlátossága miatt lehetetlen. | ||
| + | |||
| + | ==Differenciálhatóság== | ||
| + | ===Definíciója=== | ||
| + | Legyen ''f'': '''R'''<sup>n</sup> <math>\supset\!\longrightarrow</math> '''R'''<sup>m</sup> és ''u'' ∈ int Dom(f). Azt mondjuk, hogy ''f'' '''differenciálható''' az ''u'' pontban, ha létezik olyan ''A'': '''R'''<sup>n</sup> <math>\to</math> '''R'''<sup>m</sup> lineáris leképezés, hogy | ||
| + | :<math>\lim\limits_{x\to u}\frac{f(x)-f(u)-\mathcal{A}(x-u)}{||x-u||_{\mathbf{R}^n}}=0_{\mathbf{R}^m}</math> | ||
| + | Ekkor ''A'' egyértelmű és az ''f'' leképezés ''u''-bent beli '''deriválttenzor'''ának vagy '''differenciál'''jának nevezzük és d''f''(''u'')-val vagy D''f''(u)-val jelöljük. Ezt a fogalmat néha ''teljes differenciál''nak, ''totális differenciál''nak vagy ''Fréchet-derivált''nak is mondjuk. | ||
| + | ===Deriváltmátrix=== | ||
| + | Vizsgáljuk mibe viszi a bázisokat d''f''(''u'') komponensleképezésenként. A d''f''(''u'') lineáris leképezés (<math>e_1</math>,<math>e_2</math>,...,<math>e_n</math>) szetenderd bázisbeli mátrixa legyen: [d''f''(''u'')] = '''A'''. Világos, hogy (d''f''(''u''))(''x'')='''A''' ''x''. Először vegyük az '''A''' első sorvektorát, '''A'''<sub>1</sub>-et és az <math>e_1</math> egységvektor mentén tartunk ''u''-hoz: ''x'' = ''u'' + ''t''<math>e_1</math>. A d''f''(''u'')-t definiáló határértékegyenlőség ekkor a következő alakot ölti: | ||
| + | :<math>0=\lim\limits_{t\to 0}\frac{f_1(u+te_1)-f_1(u)-\mathbf{A}_1\cdot(te_1)}{t}=</math> | ||
| + | :::<math>=\lim\limits_{t\to 0}\frac{f_1(u+te_1)-f_1(u)-t\mathbf{A}_1\cdot(e_1)}{t}=</math> | ||
| + | :::<math>=-\mathbf{A}_1\cdot e_1+\lim\limits_{t\to 0}\frac{f_1(u+te_1)-f_1(u)}{t}</math> | ||
| + | azaz | ||
| + | :<math>\mathbf{A}_1\cdot e_1=\lim\limits_{t\to 0}\frac{f_1(u+te_1)-f_1(u)}{t}=\partial_1 f_1(u)</math> | ||
| + | vagyis ''f'' első koordinátafüggvényének <math>f_1</math>-nek az első változó szerinti parciális deriváltja az ''u'' pontban. A többi mátrixelemet ugyanígy: | ||
| + | |||
| + | :<math>[\mathrm{d}f(u)]=\mathbf{J}^f(u)=\begin{bmatrix} | ||
| + | \partial_1 f_1(u) & \partial_2 f_1(u) & \dots & \partial_n f_1(u)\\ | ||
| + | \partial_1 f_2(u) & \partial_2 f_2(u) & \dots & \partial_n f_2(u)\\ | ||
| + | \vdots & \vdots & \ddots & \vdots \\ | ||
| + | \partial_1 f_m(u) & \partial_2 f_m(u) & \dots & \partial_n f_m(u)\\ | ||
| + | \end{bmatrix}</math> | ||
| + | amelyet '''Jacobi-mátrix'''nak nevezünk. | ||
| + | |||
| + | ===Lineáris, konstans és affin függvény deriváltja=== | ||
| + | Az ''A'' : '''R'''<sup>n</sup> <math>\to</math> '''R'''<sup>m</sup> lineáris leképezés differenciálható és differenciálja minden pontban saját maga. | ||
| + | |||
| + | ''Ugyanis, '' legyen ''u'' ∈ '''R'''<sup>n</sup>. Ekkor | ||
| + | |||
| + | :<math>\lim\limits_{x\to u}\frac{\mathcal{A}(x)-\mathcal{A}(u)-\mathcal{A}(x-u)}{||x-u||}=\lim\limits_{x\to u}0=0</math> | ||
| + | |||
| + | c konstans függény esetén az d''c''(''u'') <math>\equiv</math> 0 alkalmas differenciálnak, mert | ||
| + | :<math>\lim\limits_{x\to u}\frac{c-c-0\cdot(x-u)}{||x-u||}=\lim\limits_{x\to u}0=0</math> | ||
| + | így világos, hogy c + ''A'' alakú affin függvények is differenciálhatóak, és differenciáljuk minden pontban az az ''A'' lineáris leképezés, melynek eltolásából az affin származik. Ezt szintén behelyettesítéssel ellenőrizhetjük. | ||
| + | |||
| + | Tehát minden ''u'' ∈ '''R'''<sup>n</sup>-re | ||
| + | :<math>\mathrm{d}\mathcal{A}(u)=\mathcal{A},\quad\quad\mathrm{d}c(u)\equiv 0,\quad\quad\mathrm{d}(b+\mathcal{A}\circ(id-a))(u)=\mathcal{A}</math> | ||
| + | |||
| + | ===Elégséges feltétel totális differenciálhatóságra=== | ||
| + | |||
| + | '''Tétel.''' Ha az ''f'':'''R'''<sup>n</sup> ⊃<math>\to</math> '''R'''<sup>m</sup> függvény minden parciális deriváltfüggvénye létezik az ''u'' egy környezetében és ''u''-ban a parciális deriváltak folytonosak, akkor ''u''-ban ''f'' differenciálható. | ||
| + | |||
| + | ==Dimenziótétel== | ||
| + | |||
| + | A dimenziótétel az lineáris leképezések magterének és képterének dimenziója közötti szoros (kiegészítő jellegű) kapcsolatra mutat rá. Most csak az <math>\mbox{ }_\mathcal{L}</math>('''R'''<sup>n</sup>;'''R'''<sup>m</sup>) leképezéseket vizsgáljuk (a tétel bármely végesdimenziós vektortérből tetszőleges vektortérbe menő lineáris függvényre is igaz.) | ||
| + | ===Magtér=== | ||
| + | Az '''A''' : '''R'''<sup>n</sup> <math>\to</math> '''R'''<sup>m</sup> lineáris leképezés magtere: | ||
| + | :<math>\mathrm{Ker}(\mathbf{A})=_{\mathrm{def}}\{v\in \mathbf{R}^n\mid \mathbf{A}v=0\}</math> | ||
| + | világos, hogy ez [[lineáris altér|altér]]. Ugyanis altér jelemzhető úgy, mint olyan részhalmaz a térben, mely zárt az összeadásra és a skalárral történő szorzásra. De Ker('''A''') ilyen, mert ''tetszőleges'' ''u'', ''v'' vektorra | ||
| + | :<math>\mathbf{A}v=0\;\land\;\mathbf{A}u=0 \quad \Rightarrow\quad\mathbf{A}v+\mathbf{A}u=0\quad \Rightarrow\quad\mathbf{A}(v+u)=0</math> | ||
| + | és | ||
| + | :<math>\mathbf{A}v=0\quad \Rightarrow\quad\lambda.(\mathbf{A}v)=0\quad \Rightarrow\quad\mathbf{A}(\lambda.v)=0</math> | ||
| + | Bázisát ('''R'''<sup>n</sup>-ben) például az '''A''' leképezés <nowiki>[</nowiki>'''A'''<nowiki>]</nowiki> mátrixának [[Gauss-elimináció]]jával és az <nowiki>[</nowiki>'''A'''<nowiki>]</nowiki>x=0 homogén egyenletrendszer megoldásával nyerhetünk (példa [[Lineáris altér#3. (magtér)|itt]]). | ||
| + | |||
| + | ===Képtér=== | ||
| + | Az '''A''' : '''R'''<sup>n</sup> <math>\to</math> '''R'''<sup>m</sup> lineáris leképezés képtere: | ||
| + | :<math>\mathrm{Im}(\mathbf{A})=_{\mathrm{def}}\{\mathbf{A}v\in \mathbf{R}^m\mid v\in \mathbf{R}^n\}</math> | ||
| + | világos, hogy ez [[lineáris altér|altér]]. Ugyanis ''alkalmas'' ''v'' és ''u'' vektorokkal: | ||
| + | :<math>\mathbf{A}v+\mathbf{A}u=\mathbf{A}(v+u)</math> | ||
| + | és | ||
| + | :<math>\lambda.(\mathbf{A}v)=\mathbf{A}(\lambda.v)</math> | ||
| + | Bázisát ('''R'''<sup>n</sup>-ben) például úgy nyerünk, hogy a '''A''' leképezés <nowiki>[</nowiki>'''A'''<nowiki>]</nowiki> mátrixának oszlopvektorai közül [[Gauss-elimináció]]val kiválasztjuk a legtöbb vektort tartalmazó lineárisan független rendszert (példa [[Lineáris altér#4. (képtér)|itt]]). | ||
| + | |||
| + | ===Tétel és bizonyítás=== | ||
| + | '''Dimenziótétel'''. Ha '''A''' : '''R'''<sup>n</sup> <math>\to</math> '''R'''<sup>m</sup> lineáris leképezés, akkor | ||
| + | :<math>\mathrm{dim}\,\mathrm{Ker}(\mathbf{A}) + \mathrm{dim}\,\mathrm{Im}(\mathbf{A}) = n</math> | ||
| + | |||
| + | ''Bizonyítás.'' Ha vesszük Ker('''A''') egy | ||
| + | :<math>B=\{b_1,...,b_k\}\,</math> | ||
| + | bázisát (Ker('''A''') dimenziója tehát ''k'') akkor világos, hogy a báziselemek képei által kifeszített | ||
| + | :<math>\langle\mathbf{A}b_1,\mathbf{A}b_2,...,\mathbf{A}b_k\rangle</math> | ||
| + | altér az '''R'''<sup>m</sup>-beli triviális {0} altér. Világos, hogy ha veszük egy Ker('''A''')-n kívüli c vektort, akkor ez már nem képeződhet a {0}-ba. Megfogalmazhatjuk tehát azt a sejtést, hogy ha B-t kibővítíjük '''R'''<sup>n</sup> bázisává, mondjuk a | ||
| + | :<math>C=\{c_1,...,c_l\}\,</math> | ||
| + | független vektorrendszerrel, akkor C elemeinek képei Im('''A''') bázisát fogja adni. Ezt fogjuk igazolni, azaz hogy | ||
| + | :<math>\langle\mathbf{A}c_1,\mathbf{A}c_2,...,\mathbf{A}c_l\rangle=\mathrm{Im}(\mathbf{A})</math> | ||
| + | és ami a tétel állítását igazolja: Im('''A''') dimenziója pont ''l''. | ||
| + | |||
| + | '''1.''' Először belátjuk, hogy { '''A'''c<sub>1</sub>, '''A'''c<sub>2</sub>, ...,'''A'''c<sub>''l''</sub> } generátorrendszere Im('''A''')-nak. Legyen | ||
| + | :<math>v=\mathbf{A}u\,</math> | ||
| + | Mivel ''B'' + ''C'' bázisa '''R'''<sup>n</sup>-nek, ezért ''u'' előáll (egyértelmű módon) | ||
| + | :<math>u=\lambda_1b_1+\lambda_2b_2+...+\lambda_kb_k+\mu_1c_1+\mu_2c_2+...+\mu_lc_l\,</math> | ||
| + | alakban. De ''u'' képében a B-beliekkel előállíthatók a {0}-ba mennek, így már a C-ből jövő képek is előállítják '''A'''u-t: | ||
| + | :<math>\mathbf{A}u=\mathbf{A}(\lambda_1b_1+\lambda_2b_2+...+\lambda_kb_k)+\mathbf{A}(\mu_1c_1+\mu_2c_2+...+\mu_lc_l)=</math> | ||
| + | :::<math>=0+\mathbf{A}(\mu_1c_1+\mu_2c_2+...+\mu_lc_l)</math> | ||
| + | :::<math>=\mu_1\mathbf{A}c_1+\mu_2\mathbf{A}c_2+...+\mu_l\mathbf{A}c_l</math> | ||
| + | '''2.''' Belátjuk, hogy { '''A'''c<sub>1</sub>, '''A'''c<sub>2</sub>, ...,'''A'''c<sub>''l''</sub> } | ||
| + | független vektorrendszer is, tehát dimenziója ''l''. | ||
| + | |||
| + | Tegyük fel, hogy vannak ''ν<sub>1</sub>, ν<sub>2</sub>, ...,ν<sub>l</sub>'' számok, melyekkel | ||
| + | :<math>\nu_1\mathbf{A}c_1+\nu_2\mathbf{A}c_2+...+\nu_l\mathbf{A}c_l=0</math> | ||
| + | A függetlenséghez az kell, hogy ''ν<sub>1</sub>, ν<sub>2</sub>, ...,ν<sub>l</sub>''-k mind nullák legyenek. Természetesen a bal oldalon kiemelhetünk '''A'''-t, tehát: | ||
| + | :<math>\mathbf{A}(\nu_1c_1+\nu_2c_2+...+\nu_lc_l)=0</math> | ||
| + | Ez viszont pontosan azt jelenti, hogy ha az | ||
| + | :<math>u=\nu_1c_1+\nu_2c_2+...+\nu_lc_l\,</math> | ||
| + | rövidítéshez folyamodunk, akkor | ||
| + | :<math>u\in \mathrm{Ker}(\mathbf{A})</math> | ||
| + | azaz az ''u'' vektor B-beli elemekkel is és C-beli elemekkel is előállítható. De ez csak úgy lehet, hogy ''u''=0, ami pedig csak akkor van, ha a ''ν<sub>1</sub>, ν<sub>2</sub>, ...,ν<sub>l</sub>'' számok mind nullák. | ||
| + | |||
| + | Mindez azt jelenti, hogy { '''A'''c<sub>1</sub>, '''A'''c<sub>2</sub>, ...,'''A'''c<sub>''l''</sub> } bázis, amiből következik, hogy az általa kifeszített altér dimenziója ''l''. De a kifeszített altér pont Im('''A'''), így azt kaptuk, hogy | ||
| + | :<math>\mathrm{dim}(\mathrm{Im}(\mathbf{A}))=n-k\,</math> | ||
| + | vagyis, amit be akartunk látni. | ||
| + | |||
| + | '''Megjegyzés.''' Világos, hogy a fenti bizonyításban a B által generál altér és a C által generált altér közös része a {0} (vagyis csak a 0-t állítják elő mindeketten). Ugyanis, ha lenne ''v'' ≠ 0, hogy | ||
| + | :<math>v=\lambda_1b_1+\lambda_2b_2+...+\lambda_kc_k\,</math> | ||
| + | és közben | ||
| + | :<math>v=\mu_1c_1+\mu_2c_2+...+\mu_kc_k\,</math> | ||
| + | akkor mindkét egyenletben a skalárok között lenne nemnulla, és a két egyenletet kivonva egymásból hpnánk, hogy a 0 vektor előáll olyan B és C-beli elemek lineáris kombinációjaként, ahol az együtthatók között van nemnulla. Ez viszont az jelentené, hogy B + C nem független rendszer (holott B + C a B egy kibővítése az '''R'''<sup>n</sup> bázisává). | ||
| + | |||
| + | Ilyenkor azt mondjuk, hogy a '''R'''<sup>n</sup> vektorteret előállítottuk a B által kifeszített és a C által kifeszített alterek '''direkt összeg'''eként: | ||
| + | :<math>\mathbf{R}^{n}=\langle B\rangle\oplus\langle C\rangle\,</math> | ||
| + | |||
| + | ==Cauchy-féle gyökkritérium== | ||
| + | '''Tétel. ''' Legyen (a<sub>n</sub>) valós számsorozat, ∑(a<sub>n</sub>) pedig a belőle képezett sor. Ekkor | ||
| + | *ha <math>\mbox{ }_{\mathrm{limsup}\sqrt[n]{|a_n|}<1}</math>, akkor ∑(a<sub>n</sub>) abszolút konvergens | ||
| + | *ha <math>\mbox{ }_{\mathrm{limsup}\sqrt[n]{|a_n|}>1}</math>, akkor ∑(a<sub>n</sub>) divergens | ||
| + | ===Bizonyítás=== | ||
| + | '''1.''' Legyen | ||
| + | :<math>c_n=\sqrt[n]{|a_n|}\,</math> | ||
| + | Ekkor ''s'' = limsup(c<sub>n</sub>) a lismesz szuperrior fogalmának deifíciója szerint az |a<sup>n</sup>| sorozat elemeinek n-edik gyökeinek (c<sub>n</sub>) sorozatának legnagyobb sűrűsödési pontja. Sűrűsödési pont, azaz ''s'' minden környezetében van a (c<sub>n</sub>) sorozatnak végtelen sok eleme, és a legnagyobb, mert nincs nála nagyobb sűrűsödési helye (c<sub>n</sub>)-nek. | ||
| + | |||
| + | ''s'' < 1 miatt vehetünk egy ''q'' számot úgy, hogy | ||
| + | :''s'' < ''q'' < 1 | ||
| + | Ekkor ''s'' "limsupsága" miatt egy adott ''M'' természetes számot követő minden ''n''-re: | ||
| + | :<math>c_n < q\,</math> | ||
| + | hiszen ha lenne végtelen sok elem, melyre ez nem telhesülne, akkor lenne ''s'' nél nagyobb sűrűsödési pont is. Tehát | ||
| + | :<math>\sqrt[n]{|a_n|} < q\,</math> | ||
| + | azaz | ||
| + | :<math>|a_n| < q^n\,</math> | ||
| + | De a (q<sup>n</sup>) mértani sorozatból képezett sor konvergens (hisz |q|<1), így a majoráns kritérium miatt a | ||
| + | :<math>\sum|a_n|\,</math> | ||
| + | sor is konvergens (merthogy a szóbanforgó mértani sor majorálja). Eszerint ∑(a<sub>n</sub>) abszolút konvergens. | ||
| + | |||
| + | '''2.''' A másik esetben, minthogy ''s'' = limsup(c<sub>n</sub>), van olyan részsorozata (c<sub>n</sub>)-nek melynek minden eleme 1-nél nagyobb egyenlő: | ||
| + | :<math>c_{n_k} \geq 1\,</math> | ||
| + | ekkor viszont | ||
| + | :<math>\sqrt[n_k]{|a_{n_k}|} \geq 1\,</math> | ||
| + | és | ||
| + | :<math>|a_{n_k}| \geq 1\,</math> | ||
| + | de a szükséges kritérium miatt ha (a<sub>n</sub>) (és vele együtt az összes részsorozata) nem a 0-hoz tart, akkor ∑(a<sub>n</sub>) nem konvergens, márpedig a fenti olyan részsorozata (a<sub>n</sub>)-nek, mely nem tarthat a 0-hoz, így ∑(a<sub>n</sub>) nem konvergens. | ||
| + | |||
| + | '''Megjegyzések.''' A bizonyításból kiderül, hogy a tétel állításának második pontjánál többet is állíthatunk. Ha ugyanis van olyan részsorozata (c<sub>n</sub>)-nek melynek minden eleme 1-nél nagyobb egyenlő, már akkor is állíthatjuk, hogy ∑(a<sub>n</sub>) nem konvergens. Ám az nem igaz, hogy ha limsup(c<sub>n</sub>) <math>\mbox{ }_{\geq}</math> 1, akkor ∑(a<sub>n</sub>) nem konvergens, ellenpélda az | ||
| + | :<math>\textstyle\sum(\frac{1}{n^2})</math> | ||
| + | sor. Ez konverges, holott az n-edik gyökök sorozatának limesz szuperiorja 1. | ||
| + | |||
| + | Az előbb említett általános divergencia kritériumon túl azonban csak azt mondhatjuk, hogy ha limsup(c<sub>n</sub>) = 1, akkor további vizsgálatokat kell végeznünk, hogy döntésre juthassunk a konvergencia/divergencia kérdésében. | ||
A lap jelenlegi, 2014. január 7., 13:22-kori változata
Tartalomjegyzék |
Többdimenziós Bolzano–Weierstrass-tétel
- Lásd még:Bolzano–Weierstrass-tétel
A többdimenziós (de nem végtelendimenziós) esetben a csúcselemes bizonyítás nem működik abban az értelmeben, hogy közvetlenül nem hivatkozhatunk rájuk, mert nincs RN-ben a műveletekkel kompatibilis rendezés. Gondolhatnók arra is, hogy komponensenként használjuk az egydimenziós B–W-tételt. Ezzel a következő a probléma. Világos, hogy létezik minden projekciósorozatra egy-egy részsorozat, mely konvergens. Ám ebből egyáltalán nem következtethetünk arra, hogy ezek metszetéből kiválasztható részsorozat. Ellenpéldaként vegyünk egy R2-ben haladó sorozatot. Tegyük fel, hogy (szerencsétlen módon) az egydimenziós B–W-tétel az első komponensek sorozatából a páros indexűeket, a második komponensek közül a páratéan indexűeket választja ki. Ekkor a kétdimenziós sorozatnak nincs olyan részsosozata, mely a komponensorozatok közös indexeikből válaszható ki, tekintve, hogy a közös indexen halmaza üres.
A fentiek miatt olyan módon kell konvergens részsorozatokat kiválasztanunk, mely bizonyosan végtelen sok közös indexel rendelkeznek. A konstrukció a következő.
Bizonyítás
Legyen
egy N komponensű sorozat, mely korlátos RN-ben. Ekkor a komponenssorozatok is korlátosak. Az egydimenziós B–W-tétel szerint az
sorozathoz létezik σ1 indexsorozat úgy, hogy az
konvergens részsorozat. Hasonlóképpen, de a
sorozatnak is van
konvergens részsorozata. Megállapíthatjuk, hogy a
sorozat szintén konvergens, mert konvergens sorozat részsorozata. Ugyanígy léteznek σ1, σ2, ..., σN indexsorozatok, hogy a
sorozatok mind konvergensek és így tetszőleges k=1...N-re
is az, ami pontosan azt jelenti, hogy az
sorozat komponensenként konvergens, azaz konvergens. A
tehát olyan indexsorozat, mely konvergens részsorozatot választ ki (an)-ből.
Ellenpélda végtelen dimenzióra
A tétel végtelen dimenziós esetben nem igaz. Vegyük példul a korlátos valós függvények
terében a szuprémumnormát:
és a belőle definiálható távolságot. Ebben az esetben a páratlan gyökkitevőjű gyökfüggvények
sorozata nem konvergens. Ez amiatt van, hogy az itteni konvergenciafogalom ugyanaz, mint a függvénysorozatok egyenletes konvergenciájának fogalma. Bár ez a függvénysorozat pontonként konvergál a szignumfüggvényhez, de a sorozat a szignumfüggvény minden környezetéből kilép. Emiatt még az is igaz, hogy egyetlen részsorozta sem lehet konvergens (azaz egyenletesen konvergens), holott a függvénysorozat maga korlátos (u.is. belefoglalható az azonosan 0 függvény 2 sugarú környezetébe).
Megjegyzés. A tétel azon iránya, mely a sorozatkompaktságot tételezi fel, igaz marad minden metrikus térben.
Weierstrass tétele
Az alábbiakban felhasználjuk a kompaktság fogalmát (és esetleg a bizonyitas egy masik variansa a Heine–Borel-tételt).
(Kompakt egy K halmaz, ha minden nyílt halmazrendszerből, melynek uniója lefedi K-t kiválasztható véges sok nyílt halmaz is, melyek véges uniója még mindig lefedi K-t.
Heine–Borel-tétel. Veges dimenzios normalt terben korlátos és zárt halmaz kompakt.)
Tétel (Weierstrass) Valós értékű, kompakt halmazon folytonos függvény felveszi minimumát és maximumát.
- (Ha f ∈ C(Rn,R), Dom(f) kompakt, akkor sup(f), inf(f) ∈ Ran(f) )
Bizonyítás.
1) Először belátjuk, hogy kompakt halmazon folytonos függvény korlátos. Legyen ugyanis ε tetszőleges pozitív szám és f értelmezési tartománya K. A folytonosság miatt K minden u eleméhez létezik δ(u) pozitív szám, hogy f a Bδ(u) környezeten belül mindvégig az (f(u)-ε,f(u)+ε) intervallumon belül marad. Ekkor a nyílt halmazokbol allo {Bδ(u)(u) : u ∈ K} rendszer lefedi K-t, ami kompakt, azaz ebből mar véges sok is lefedi K-t. Legyen ez {Bδ(u)(u) : u ∈ F}, ahol tehát F ⊆ K véges. Ezek képei mind a (f(u)-ε,f(u)+ε) (u∈F) intervallumokban vannak, így a {(f(u)-ε,f(u)+ε) : u ∈ F} véges intervallumrendszer lefedi Ran(f)-et. Tehát f a "legmagasabb" intervallum felső határa és a "legalacsonyabb" intervallum alsó határa közé esik.
2) Belátjuk, hogy f felveszi a szuprémumát (és ugyanígy az infimumát is). Legyen S := sup(f) (azaz f értékkészletének legkisebb felső korlátja). Ekkor a g : K  R, x
R, x  S-f(x)függvény nemnegatív értékeket vesz föl. Ha f nem venné fel a szuprémumát, akkor g pozitív lenne. Ekkor értelmezhető lenne a
S-f(x)függvény nemnegatív értékeket vesz föl. Ha f nem venné fel a szuprémumát, akkor g pozitív lenne. Ekkor értelmezhető lenne a
függvény. h mert folytonos függvényekből van folytonosságot megőrző módon összetéve. Az 1) pont szerint korlátos is, ami azonban ellentmond annak, hogy S a szuprémum, mert f minden határon túl megközelíti S-et. Ugyanis minden S - 1/n számhoz létezik olyan xn ∈ K, hogy f(xn) > S - 1/n. Létezik tehát olyan (xn) K-ban haladó sorozat, melyre f(x_n) alulrúl az S-hez tart. Ám, ekkor az 1/(S-f(xn)) a +∞-hez tart, ami h korlátossága miatt lehetetlen.
Differenciálhatóság
Definíciója
Legyen f: Rn  Rm és u ∈ int Dom(f). Azt mondjuk, hogy f differenciálható az u pontban, ha létezik olyan A: Rn
Rm és u ∈ int Dom(f). Azt mondjuk, hogy f differenciálható az u pontban, ha létezik olyan A: Rn  Rm lineáris leképezés, hogy
Rm lineáris leképezés, hogy
Ekkor A egyértelmű és az f leképezés u-bent beli deriválttenzorának vagy differenciáljának nevezzük és df(u)-val vagy Df(u)-val jelöljük. Ezt a fogalmat néha teljes differenciálnak, totális differenciálnak vagy Fréchet-deriváltnak is mondjuk.
Deriváltmátrix
Vizsgáljuk mibe viszi a bázisokat df(u) komponensleképezésenként. A df(u) lineáris leképezés (e1,e2,...,en) szetenderd bázisbeli mátrixa legyen: [df(u)] = A. Világos, hogy (df(u))(x)=A x. Először vegyük az A első sorvektorát, A1-et és az e1 egységvektor mentén tartunk u-hoz: x = u + te1. A df(u)-t definiáló határértékegyenlőség ekkor a következő alakot ölti:
azaz
vagyis f első koordinátafüggvényének f1-nek az első változó szerinti parciális deriváltja az u pontban. A többi mátrixelemet ugyanígy:
amelyet Jacobi-mátrixnak nevezünk.
Lineáris, konstans és affin függvény deriváltja
Az A : Rn  Rm lineáris leképezés differenciálható és differenciálja minden pontban saját maga.
Rm lineáris leképezés differenciálható és differenciálja minden pontban saját maga.
Ugyanis, legyen u ∈ Rn. Ekkor
c konstans függény esetén az dc(u)  0 alkalmas differenciálnak, mert
0 alkalmas differenciálnak, mert
így világos, hogy c + A alakú affin függvények is differenciálhatóak, és differenciáljuk minden pontban az az A lineáris leképezés, melynek eltolásából az affin származik. Ezt szintén behelyettesítéssel ellenőrizhetjük.
Tehát minden u ∈ Rn-re
Elégséges feltétel totális differenciálhatóságra
Tétel. Ha az f:Rn ⊃ Rm függvény minden parciális deriváltfüggvénye létezik az u egy környezetében és u-ban a parciális deriváltak folytonosak, akkor u-ban f differenciálható.
Rm függvény minden parciális deriváltfüggvénye létezik az u egy környezetében és u-ban a parciális deriváltak folytonosak, akkor u-ban f differenciálható.
Dimenziótétel
A dimenziótétel az lineáris leképezések magterének és képterének dimenziója közötti szoros (kiegészítő jellegű) kapcsolatra mutat rá. Most csak az 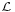 (Rn;Rm) leképezéseket vizsgáljuk (a tétel bármely végesdimenziós vektortérből tetszőleges vektortérbe menő lineáris függvényre is igaz.)
(Rn;Rm) leképezéseket vizsgáljuk (a tétel bármely végesdimenziós vektortérből tetszőleges vektortérbe menő lineáris függvényre is igaz.)
Magtér
Az A : Rn  Rm lineáris leképezés magtere:
Rm lineáris leképezés magtere:
világos, hogy ez altér. Ugyanis altér jelemzhető úgy, mint olyan részhalmaz a térben, mely zárt az összeadásra és a skalárral történő szorzásra. De Ker(A) ilyen, mert tetszőleges u, v vektorra
és
Bázisát (Rn-ben) például az A leképezés [A] mátrixának Gauss-eliminációjával és az [A]x=0 homogén egyenletrendszer megoldásával nyerhetünk (példa itt).
Képtér
Az A : Rn  Rm lineáris leképezés képtere:
Rm lineáris leképezés képtere:
világos, hogy ez altér. Ugyanis alkalmas v és u vektorokkal:
és
Bázisát (Rn-ben) például úgy nyerünk, hogy a A leképezés [A] mátrixának oszlopvektorai közül Gauss-eliminációval kiválasztjuk a legtöbb vektort tartalmazó lineárisan független rendszert (példa itt).
Tétel és bizonyítás
Dimenziótétel. Ha A : Rn  Rm lineáris leképezés, akkor
Rm lineáris leképezés, akkor
Bizonyítás. Ha vesszük Ker(A) egy
bázisát (Ker(A) dimenziója tehát k) akkor világos, hogy a báziselemek képei által kifeszített
altér az Rm-beli triviális {0} altér. Világos, hogy ha veszük egy Ker(A)-n kívüli c vektort, akkor ez már nem képeződhet a {0}-ba. Megfogalmazhatjuk tehát azt a sejtést, hogy ha B-t kibővítíjük Rn bázisává, mondjuk a
független vektorrendszerrel, akkor C elemeinek képei Im(A) bázisát fogja adni. Ezt fogjuk igazolni, azaz hogy
és ami a tétel állítását igazolja: Im(A) dimenziója pont l.
1. Először belátjuk, hogy { Ac1, Ac2, ...,Acl } generátorrendszere Im(A)-nak. Legyen
Mivel B + C bázisa Rn-nek, ezért u előáll (egyértelmű módon)
alakban. De u képében a B-beliekkel előállíthatók a {0}-ba mennek, így már a C-ből jövő képek is előállítják Au-t:
2. Belátjuk, hogy { Ac1, Ac2, ...,Acl } független vektorrendszer is, tehát dimenziója l.
Tegyük fel, hogy vannak ν1, ν2, ...,νl számok, melyekkel
A függetlenséghez az kell, hogy ν1, ν2, ...,νl-k mind nullák legyenek. Természetesen a bal oldalon kiemelhetünk A-t, tehát:
Ez viszont pontosan azt jelenti, hogy ha az
rövidítéshez folyamodunk, akkor
azaz az u vektor B-beli elemekkel is és C-beli elemekkel is előállítható. De ez csak úgy lehet, hogy u=0, ami pedig csak akkor van, ha a ν1, ν2, ...,νl számok mind nullák.
Mindez azt jelenti, hogy { Ac1, Ac2, ...,Acl } bázis, amiből következik, hogy az általa kifeszített altér dimenziója l. De a kifeszített altér pont Im(A), így azt kaptuk, hogy
vagyis, amit be akartunk látni.
Megjegyzés. Világos, hogy a fenti bizonyításban a B által generál altér és a C által generált altér közös része a {0} (vagyis csak a 0-t állítják elő mindeketten). Ugyanis, ha lenne v ≠ 0, hogy
és közben
akkor mindkét egyenletben a skalárok között lenne nemnulla, és a két egyenletet kivonva egymásból hpnánk, hogy a 0 vektor előáll olyan B és C-beli elemek lineáris kombinációjaként, ahol az együtthatók között van nemnulla. Ez viszont az jelentené, hogy B + C nem független rendszer (holott B + C a B egy kibővítése az Rn bázisává).
Ilyenkor azt mondjuk, hogy a Rn vektorteret előállítottuk a B által kifeszített és a C által kifeszített alterek direkt összegeként:
Cauchy-féle gyökkritérium
Tétel. Legyen (an) valós számsorozat, ∑(an) pedig a belőle képezett sor. Ekkor
- ha
![\mbox{ }_{\mathrm{limsup}\sqrt[n]{|a_n|}<1}](/upload/math/2/a/2/2a2c0ff510cb6780177e06a528d0b021.png) , akkor ∑(an) abszolút konvergens
, akkor ∑(an) abszolút konvergens
- ha
![\mbox{ }_{\mathrm{limsup}\sqrt[n]{|a_n|}>1}](/upload/math/f/a/7/fa7619a6b425862203c91113c4990925.png) , akkor ∑(an) divergens
, akkor ∑(an) divergens
Bizonyítás
1. Legyen
Ekkor s = limsup(cn) a lismesz szuperrior fogalmának deifíciója szerint az |an| sorozat elemeinek n-edik gyökeinek (cn) sorozatának legnagyobb sűrűsödési pontja. Sűrűsödési pont, azaz s minden környezetében van a (cn) sorozatnak végtelen sok eleme, és a legnagyobb, mert nincs nála nagyobb sűrűsödési helye (cn)-nek.
s < 1 miatt vehetünk egy q számot úgy, hogy
- s < q < 1
Ekkor s "limsupsága" miatt egy adott M természetes számot követő minden n-re:
hiszen ha lenne végtelen sok elem, melyre ez nem telhesülne, akkor lenne s nél nagyobb sűrűsödési pont is. Tehát
azaz
De a (qn) mértani sorozatból képezett sor konvergens (hisz |q|<1), így a majoráns kritérium miatt a
sor is konvergens (merthogy a szóbanforgó mértani sor majorálja). Eszerint ∑(an) abszolút konvergens.
2. A másik esetben, minthogy s = limsup(cn), van olyan részsorozata (cn)-nek melynek minden eleme 1-nél nagyobb egyenlő:
ekkor viszont
és
de a szükséges kritérium miatt ha (an) (és vele együtt az összes részsorozata) nem a 0-hoz tart, akkor ∑(an) nem konvergens, márpedig a fenti olyan részsorozata (an)-nek, mely nem tarthat a 0-hoz, így ∑(an) nem konvergens.
Megjegyzések. A bizonyításból kiderül, hogy a tétel állításának második pontjánál többet is állíthatunk. Ha ugyanis van olyan részsorozata (cn)-nek melynek minden eleme 1-nél nagyobb egyenlő, már akkor is állíthatjuk, hogy ∑(an) nem konvergens. Ám az nem igaz, hogy ha limsup(cn) 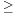 1, akkor ∑(an) nem konvergens, ellenpélda az
1, akkor ∑(an) nem konvergens, ellenpélda az
sor. Ez konverges, holott az n-edik gyökök sorozatának limesz szuperiorja 1.
Az előbb említett általános divergencia kritériumon túl azonban csak azt mondhatjuk, hogy ha limsup(cn) = 1, akkor további vizsgálatokat kell végeznünk, hogy döntésre juthassunk a konvergencia/divergencia kérdésében.
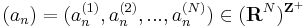
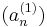
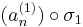
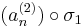
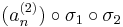
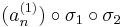

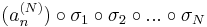
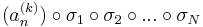
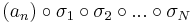
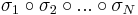
![\mathrm{B}([-1,+1],\mathbf{R})\,](/upload/math/6/f/8/6f81ef1e657e662d5f30dcfba319be40.png)
![||f||=_{\mathrm{def}}\sup\{|f(x)|\mid x\in [-1,+1]\}\,](/upload/math/9/e/c/9ec0abff769966a02d1869c5efc9881e.png)
![f_n=\sqrt[2n+1]{.\;}\quad\quad (f_n(x)=\sqrt[2n+1]{x})](/upload/math/6/8/1/68142b19ef9f58a8e151b2ea4973d681.png)
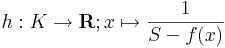
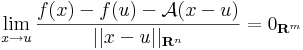
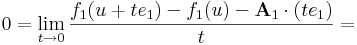
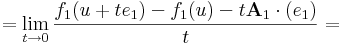
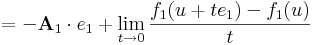
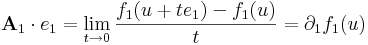
![[\mathrm{d}f(u)]=\mathbf{J}^f(u)=\begin{bmatrix}
\partial_1 f_1(u) & \partial_2 f_1(u) & \dots & \partial_n f_1(u)\\
\partial_1 f_2(u) & \partial_2 f_2(u) & \dots & \partial_n f_2(u)\\
\vdots & \vdots & \ddots & \vdots \\
\partial_1 f_m(u) & \partial_2 f_m(u) & \dots & \partial_n f_m(u)\\
\end{bmatrix}](/upload/math/b/c/8/bc8c1cf3c3d6f5032a7858552cc82a3a.png)
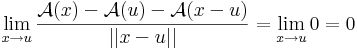
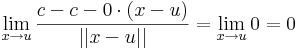

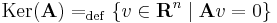
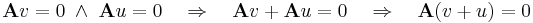
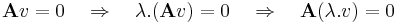
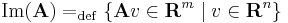


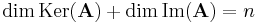
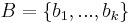
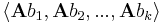
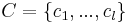
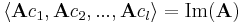
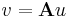
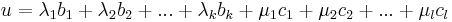
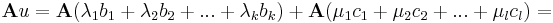
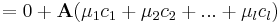
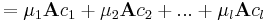
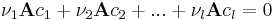
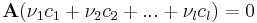
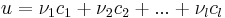
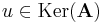
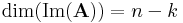
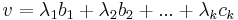
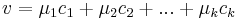
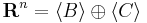
![c_n=\sqrt[n]{|a_n|}\,](/upload/math/b/3/c/b3c93c4892c869fcaa0541f02c6420cc.png)
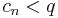
![\sqrt[n]{|a_n|} < q\,](/upload/math/8/e/d/8ed01181ef1c12da8e399eba5cdebaec.png)
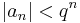
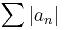
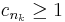
![\sqrt[n_k]{|a_{n_k}|} \geq 1\,](/upload/math/2/c/e/2ced0800302863bba53c806d141a7036.png)