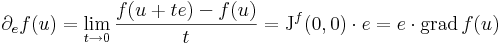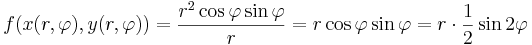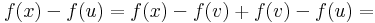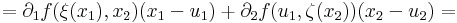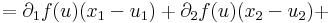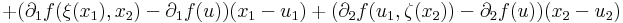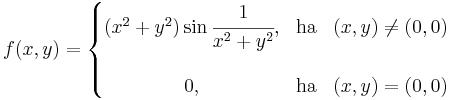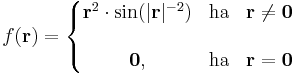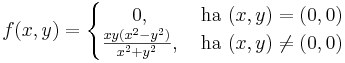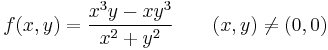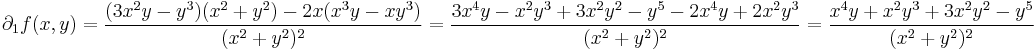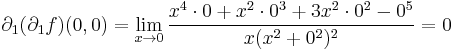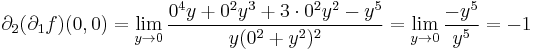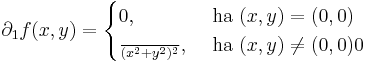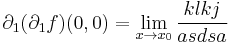Matematika A2a 2008/3. gyakorlat
- Ez az szócikk a Matematika A2a 2008 alszócikke.
Ezen a konkrét gyakorlaton konkrét függvények konkrét folytonosságát és konkrét határértékét vizsgáljuk meg konkrét módon.
Tartalomjegyzék |
További példák
1. Hol létezik határértéke az alábbi függvényeknek?
- a)
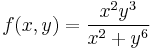
- b)
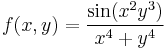 (Használjuk az
(Használjuk az ![\frac{\sin \vartheta}{\vartheta}\xrightarrow[\vartheta\to 0]\,1](/upload/math/3/3/8/338651eec220434dd235b495979ac806.png) határértéket.)
határértéket.)
- c)
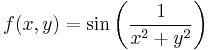
- d)
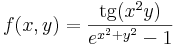
- e)
![f(x,y)=\frac{x^2y}{\sqrt[5]{x^2+y^2}}](/upload/math/3/8/6/38613f6a1f08dc2512f6baea3466a691.png)
- f)
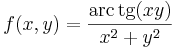
- g)
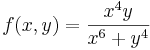
- h)
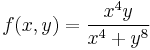
- i)
![f(x,y)=\frac{x^2y}{\sqrt[3]{x^4+y^8}}](/upload/math/c/9/c/c9cc62455e9f4d640769537bf54ee8d9.png)
- k)
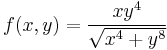
Parciális deriváltak
Definíció. Legyen f: Rn 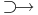 R, u ∈ int Dom(f). Azt mondjuk, hogy f parciálisan differenciálható az u pontban a xi változó szerint, ha az
R, u ∈ int Dom(f). Azt mondjuk, hogy f parciálisan differenciálható az u pontban a xi változó szerint, ha az
egyváltozós valós függvény differenciálható az ui pontban. Ekkor a fenti függvény ui-beli deriváltját
jelöli.
Példa:
Feladat. Parciálisan deriválható-e az
a (0,0)-ban?
Feladat. Parciálisan deriválható-e az
a (0,0)-ban?
Lineáris leképezések
A V1 és V2 vektorterek között ható A leképezést akkor nevezünk lineárisnak, ha teljesül minden λ, μ ∈ R és v, u ∈ V1
A definícióból rögtön következik, hogy a nulla vektor képe nulla:
viszont más elem a V2 nem feltétlenül vétetik föl.
Véges dimenziós terek közti lineáris leképezés a bázis választásával egyértelműen jellemezhető az alábbi mátrixszal.
ahol B = (b1,b2,…,bn) a V1 egy bázisa, C az V2 bázisa, a mátrix oszlopai pedig a B elemeinek 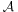 általi képvektoraiból, mint oszlopvektorokból áll. Ha
általi képvektoraiból, mint oszlopvektorokból áll. Ha 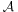 V
V  V típusú, akkor csak
V típusú, akkor csak ![\mbox{ }_{[\mathcal{A}]_B}](/upload/math/1/5/6/156d0043945fe751a951df3818cbfb93.png) -t szokás írni, ha pedig pusztán
-t szokás írni, ha pedig pusztán ![\mbox{ }_{[\mathcal{A}]}](/upload/math/a/b/0/ab06c27145a3fa90b92cfb08c9e0d4fe.png) -t írnak, akkor az azt jelenti, hogy a Rn sztenderd bázisáról van szó, azaz a
-t írnak, akkor az azt jelenti, hogy a Rn sztenderd bázisáról van szó, azaz a
vektorrendszerről.
Példák
1. Forgatás az origo körül φ szöggel:
Világos, hogy ez invertálható leképezés és az inverze a -φ szögű forgatás.
2. Tükrözés a φ szőgű egyenesre.
Világos, hogy ez is invertálható és inverze saját maga.
Ezek ortogonális transzformációk, azaz a transzponáltjuk az inverzük. Speciálisan a tükrözés szimmetrikus leképezés, mert mátrixa szimmetrikus. Sőt, ezek alkotják a síkon az összes ortogonális transzformációt.
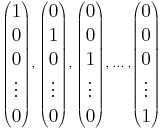
3. Deriváló operáció. Legyen V a legfeljebb másodfokú polinomfüggvények tere. Ekkor a
lineáris leképezés:
Bázis V-ben: {1, x, x2}, ezért a mátrixa:
Világos, hogy a leképezés képzere nem a teljes V, hanem annak egy altere (a legfeljebb elsőfokú polinomfüggvények tere) és nem csak a 0 polinom képe 0, hanem minden konstans polinomé.
Differenciálhatóság
Definíció és folytonosság
Azt mondjuk, hogy az 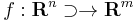 függvény (totálisan) differenciálható az
függvény (totálisan) differenciálható az 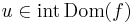 pontban, ha létezik olyan
pontban, ha létezik olyan 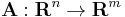 lineáris leképezés, hogy
lineáris leképezés, hogy
Ez az A lineáris leképezés egyértelmű és ha kell, df(u)-val jelöljük.
Egy ezzel ekvivalens megfogalmazást is kimondunk, ami rendkívül jól használható feltétel lesz később. A fenti f differenciálható az értelmezési tartományának belső u pontjában, ha létezik olyan 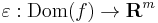 függvény és
függvény és 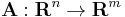 lineáris leképezés, hogy
lineáris leképezés, hogy
- 1) minden
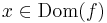 -re:
-re: 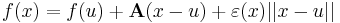 és
és
- 2)
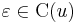 és
és 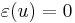 .
.
Ebből rögtön következik, hogy differenciálható függvény folytonos.
Deriválható-e az
függvény?
Parciális differenciálhatóság és differenciálhatóság
Ha f:Rn Rm (totálisan) differenciálható az értelmezési tartományának u belső pontjában, akkor f parciálisan differenciálható u-ban és df(u) mátrixa a sztenderd bázisban:
Rm (totálisan) differenciálható az értelmezési tartományának u belső pontjában, akkor f parciálisan differenciálható u-ban és df(u) mátrixa a sztenderd bázisban:
Bizonyítás. Bőven elég egy komponensfüggvénnyel rendelkező függvényre igazolni. A határérték és függvénykompozíció kapcsolatára vonatkozó tétel szerint, ha a belső pontja a Dom(g)-nek, g injektív és g(a) belső pontja Dom(h)-nak és létezik g-nek (véges) határértéke a-ban és h-nak a g-nek az a-beli határértékében, akkor a hog-nek is létezik a-ban határértéke és
Innen a g:x(t) = u + tei függvénnyel(, ahol ei az i-edik sztenderd báziselem) és az a = 0 ponttal teljesül, hogy
Példa. Tekintsük az
Ekkor
Viszont g nem totálisan diffható, mert a (t,t) mentén a (0,0)-ba tartva:
ami nem létezik.
Persze g nem folytonos, és így nem is lehet totálisan differenciálható.
Példa. ![f(x,y)=\sqrt[3]{x^4+y^4}](/upload/math/2/c/3/2c335aa3afa0bf0f307a9be26d78c087.png)
Iránymenti deriválhatóság és differenciálhatóság
Ha e tetszőleges egységvektor, akkor
Példa.
Ekkor
Ha tehát differenciálható, akkor az iránymenti deriváltak (Gateau-deriváltak) is léteznek (e egységvektor):
Ám, polárkoordinátákra áttérve:
φ = π/4-et és π + π/4-et véve a vetületfüggvény a
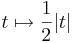 ,
,
ami nem differenciálható a 0-ban.
Megjegyzés. Persze abból, hogy az összes iránymenti derivált létezik, abból nem következik, hogy a függvény totálisan deriválható:
Folytonos parciális differenciálhatóság
Megfordításról a következő esetben beszélhetünk.
Tétel. Ha az f:Rn ⊃ Rm függvény minden parciális deriváltfüggvénye létezik az u egy környezetében és u-ban a parciális deriváltak folytonosak, akkor u-ban f differenciálható. (Sőt, folytonosan differenciálható.)
Rm függvény minden parciális deriváltfüggvénye létezik az u egy környezetében és u-ban a parciális deriváltak folytonosak, akkor u-ban f differenciálható. (Sőt, folytonosan differenciálható.)
Bizonyítás. Elegendő az m = 1 esetet vizsgálni. Továbbá a bizonyítás elve nem változik, ha csak az n = 2 esetet tekintjük. Legyen x az u mondott környezetéből vett pont, és x = (x1,x2), v=(u1,x2), u=(u1,u2) Ekkor az [x,v] szakaszon ∂1f-hez a Lagrange-féle középértéktétel miatt létezik olyan ξ(x1)∈[x1,u1] szám, és a [v,u] szakaszon ∂2f-hez ζ(x2)∈[x2,u2] szám, hogy
itt az
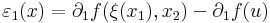 és
és 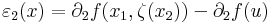
függvények folytonosak u-ban (még ha a ξ, ζ függvények nem is azok), és értékük az u-ban 0. Világos, hogy ez azt jelenti, hogy f differenciálható u-ban.
Világos, hogy a parciális deriváltak folytonossága szükséges a fenti tételben. Az alábbi példában léteznek a parciális deriváltfüggvények az u egy környzetében, de az u-ban nem folytonosak.
Példa
A differenciálhatóság azonban nem elég ahhoz, hogy a parciális deriváltak folytonosak legyenek.
Az
differenciálható, hiszen ez az
függvény és r ≠ 0-ban:
Példa
1) Polárkoordinátásan könnyen kijön, hogy ez a függvény totálisan deriválható. Parciális deriváltjai a 0-ban: 0.
2) Melyek a második parciális deriváltjai a 0-ban?
| 2. gyakorlat | pótló gyakorlat |
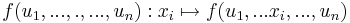
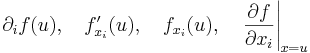
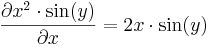
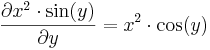
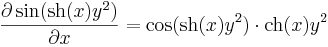
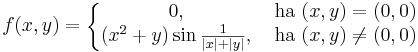

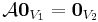
![[\mathcal{A}]_{B,C} = \begin{bmatrix}
\begin{matrix}\vert \\ \vert \\ \mathcal{A}\mathbf{b}_1 \\ \vert \\ \vert \end{matrix}& \begin{matrix}\vert \\ \vert \\ \mathcal{A}\mathbf{b}_2 \\ \vert \\ \vert \end{matrix} & ... & \begin{matrix}\vert \\ \vert \\ \mathcal{A}\mathbf{b}_n \\ \vert \\ \vert \end{matrix}
\end{bmatrix}](/upload/math/e/2/1/e218d5327c820937af47e217f5212ec7.png)
![[\mathcal{F}_\varphi]=\begin{bmatrix}\cos\varphi & -\sin\varphi \\ \sin\varphi & \cos\varphi \end{bmatrix}](/upload/math/1/b/d/1bd899a86970ed93aad1b307d1af4e0b.png)
![[\mathcal{T}_\varphi]=\begin{bmatrix}\cos(2\varphi) & \sin(2\varphi) \\ \sin(2\varphi) & -\cos(2\varphi) \end{bmatrix}](/upload/math/4/f/3/4f3d3c1c23cacad098bf0349140e0d0f.png)
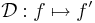
![[\mathcal{D}]=
\begin{bmatrix}
0 & 1 & 0 \\
0 & 0 & 2\\
0 & 0 & 0
\end{bmatrix}](/upload/math/a/7/a/a7ad5c2aa1f95e6c92807ec3550700c1.png)
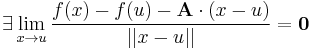
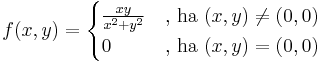
![[\mathrm{d}f(u)]=\begin{bmatrix}\partial_{x_1}f_1 &\dots &\partial_{x_n}f_1\\\vdots & &\\\partial_{x_1}f_m &\dots &\partial_{x_n}f_m\end{bmatrix}](/upload/math/f/3/3/f33a5338c1cb003ffd43860238ccda30.png)
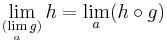
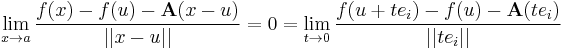
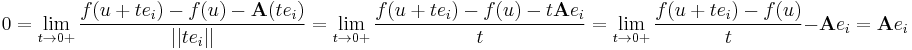
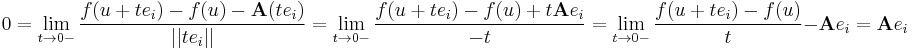
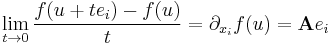
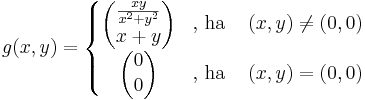
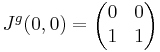
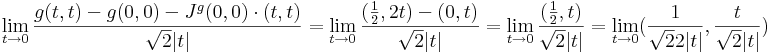
![\lim\limits_{t\to 0}\frac{f(u+te)-f(u)}{t}=\partial_{e}f(u)=[\mathrm{grad}\,f(u)]\cdot e=[\nabla f(u)]\cdot e](/upload/math/6/8/f/68fffe8f513e9e456ec239b3c12e2069.png)
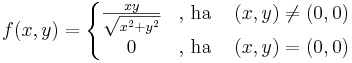
![\mathrm{J}^f(0,0)=[0, 0]\,](/upload/math/5/8/4/5844bda58422be338e9d02beef5b1e3e.png)