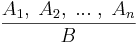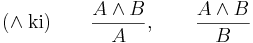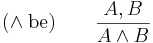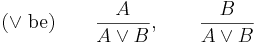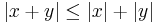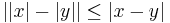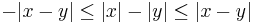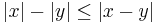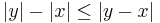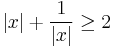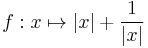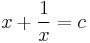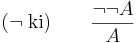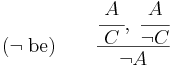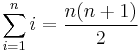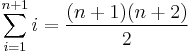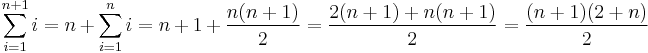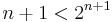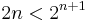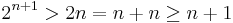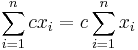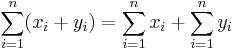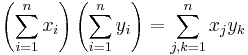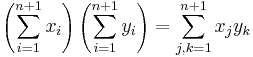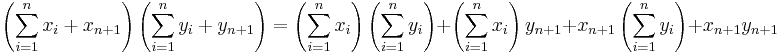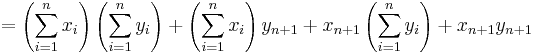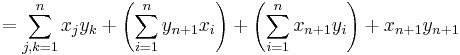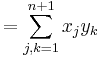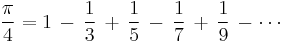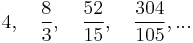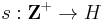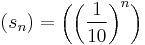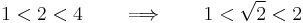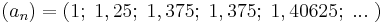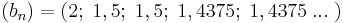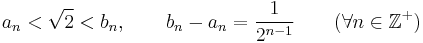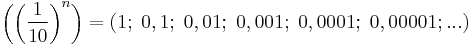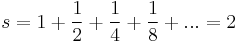Matematikai előismeretek 1.
Tartalomjegyzék |
Logikai következtetési sémák
Ha A1, A2, ..., An, B mondatok, akkor azt mondjuk, hogy az
szimbólummal jelölt következtetés helyes, ha minden olyan esetben, amikor az A1, A2, ..., An mondatok (az úgy nevezett premisszák vagy feltételek) mindegyike igaz, akkor a B mondat, azaz a konkúzió (következmény) is igaz.
A helyes következtetések listája elég nagy, ám vannak bizonyos tekintetben alapvetőnek tekinthető kövekeztetések, melyeket könnyen lehet kategorizálni a bevezetési és kiküszöbölési szabályok módszere szerint.
Direkt következtetések
A legegyszerűbb eset az és (jelben  ) mondatoperátorral összekötött összetett mondatokra vonatkozó bevezetési és kiküszöbölési szabály. Egy mondatoperátor kiküszöbölési szabálya lényegében az, hogy megadja, mire következtethetünk az adott operátorral összekötött mondatokból, jelen esetben például A és B összetett mondatból. Eszerint:
) mondatoperátorral összekötött összetett mondatokra vonatkozó bevezetési és kiküszöbölési szabály. Egy mondatoperátor kiküszöbölési szabálya lényegében az, hogy megadja, mire következtethetünk az adott operátorral összekötött mondatokból, jelen esetben például A és B összetett mondatból. Eszerint:
Azaz, ha tudjuk, hogy A és B igaz, akkor jogos kijelentenünk, akár A, akár B igazságának fennállását. A bevezetési szabály azt adja meg, hogy miből következtethetünk az adott összetételre. Világos, hogy a helyes következtetés fenti értelemezése szerint minden olyan esetben, amikor az {A, B} premisszapár minden tagja igaz, levonhatjuk az A és B konklúziót:
A vagy (jelben:  ) bevezetési szabálya szintén nyilvánvaló:
) bevezetési szabálya szintén nyilvánvaló:
Ezzel szemben a kiküszöbölési szabályának tárgyalásával máris belefutottunk a logikafilozófia ingoványába, ezt persze nem tárgyaljuk, csak magát a következtetési szabályt. A vagy kiküszöbölési szabályát az esetszétválasztás szabályának nevezzük:
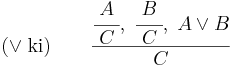 az esetszétválasztás szabálya
az esetszétválasztás szabálya
Azaz ha A-ból következik a C és a B-ből is következik a C, továbbá az A és a B közül legalább az egyik igaz (ez a klasszikus vagy: nem feltétlenül tudjuk, melyik igaz, csak azt, hogy az egyik), akkor a C biztos igaz.
Abszolútérték
Példa (Háromszög egyenlőtlenség) Minden valós x, y számra:
és egyenlőség pontosan akkor áll fenn, ha x, y azonos előjelű.
Mo. Az abszolútérték definíciója: |x|=x, ha x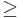 0, és |x|=-x, ha x<0. Esetszétválasztással bizonyítunk. Triviális eset: x=y, akkor |2x|=2|x|=|x|+|x|. Lényeges eset: x≠y. Ekkor az általánosság megszorítása nélkül feltehető, hogy x<y, mert az egyenlőtlenség az x és y felcserélésére nézve szimmetrikus. Ekkor két eset lehetséges:
0, és |x|=-x, ha x<0. Esetszétválasztással bizonyítunk. Triviális eset: x=y, akkor |2x|=2|x|=|x|+|x|. Lényeges eset: x≠y. Ekkor az általánosság megszorítása nélkül feltehető, hogy x<y, mert az egyenlőtlenség az x és y felcserélésére nézve szimmetrikus. Ekkor két eset lehetséges:
1) x, y előjele azonos: ekkor vagy |x|+|y|=x+y=|x+y| vagy |x|+|y|=-x-y=|x+y|,
2) x, y előjele kölönböző. Ekkor |x|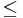 |y| és ekkor |y+x|<|y|
|y| és ekkor |y+x|<|y|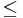 |x|+|y| vagy ellenkezőleg és akkor |x+y|<|x|
|x|+|y| vagy ellenkezőleg és akkor |x+y|<|x|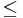 |x|+|y|.
|x|+|y|.
A utolsó esetben egyenlőtlenség növelésére, csökkentésére láttunk példát. Fontos jellemzése az abszolútértékes egyelőltelnségnek a következő: |a|<r, akkor és csak akkor, ha -r<a<+r. Ennek segítségével beláthatjuk, hogy
1. Feladat. Minden valós x, y számra:
és egyenlőség pontosan akkor áll fenn, ha x, y előjele azonos.
Mo. Az előzőek szerint azt kell belátjunk, hogy
Valóban. Minden x-re:
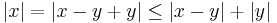 és emiatt:
és emiatt:
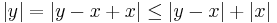
azaz
amely kettő egyszerre pont a keresett egyenlőtlenség.
2. Feladat (Szélsőérték-keresés Descartes módszerével) Igazoljuk, hogy minden x nemnulla valós számra
és egyenlőség pontosan akkor áll fenn, ha |x|=1.
Mo. Mivel az
függvény páros (grafikonja szimmetrikus az y tengelyre) ezért elegendő belátni pozitívokra. Keressük meg azt a pontot, ahol a f(x) és a c konstans egyetlen pontban metszi egymást! Ez pontosan akkor van, ha az f(x)=c egyenletnek két egybeeső gyöke van:
Megj.: f páros, ha minden x∈Dom(f)-re -x∈Dom(f) és f(x)=f(-x).
Indirekt bizonyítás
A tagadás (negáció) kiküszöbölési szabálya az úgy nevezett kettős tagadás törlésének szabálya:
A bevezetési szabálya pedig az úgy nevezett redukció ad abszurdum.
Példa. Igazoljuk, hogy a valós számok halmaza nem sorolható fel egyetlen végtelen sorozatban.
Mo. Indirekten bizonyítunk, a nevezetes Cantor-féle átlós eljárást fogjuk használni. Nos, az biztos, hogy növekvő sorrendbe nem tudjuk felsorolni :) Tekintsük a [0,1] intervallumot és a valós számok tizedestört alakjait. Tegyük fel, hogy van és vegyünk egy tetszőleges felsorolást, (xk)-t:
- x1 = 0, 5 1 0 5 1 1 0 …
- x2 = 0, 4 2 3 2 0 4 3 …
- x3 = 0, 8 2 4 5 0 2 6 …
- x4 = 0, 2 3 3 0 1 2 6 …
- x5 = 0, 4 1 0 7 2 4 6 …
- x6 = 0, 9 9 3 7 8 3 8 …
- x7 = 0, 0 1 0 5 1 3 5 …
- …
Tekintsük a k-adik valós szám k-adik tizedesjegyét, jelöljük ezt xkk-val!
- x1 = 0, 5 1 0 5 1 1 0 …
- x2 = 0, 4 2 3 2 0 4 3 …
- x3 = 0, 8 2 4 5 0 2 6 …
- x4 = 0, 2 3 3 0 1 2 6 …
- x5 = 0, 4 1 0 7 2 4 6 …
- x6 = 0, 9 9 3 7 8 3 8 …
- x7 = 0, 0 1 0 5 1 3 5 …
- …
Most konstruálunk egy tizedestört előállítást. az r szám k-adik jegye legyen 2, ha xkk nem 2 és legyen 0, ha xkk=2. A fenti sorozattal például r=0,2022022... Világos, hogy r valós számot ír le. Most belátjuk, hogy r nem szerepelhet a listában. Tegyük ugyanis fel, hogy valamely m-re xm=r. Ekkor, ha xmm=2, akkor r definíciója miatt xmm=0. De ha xmm nem 2, akkor xmm=2, ami ellentmondás. Tehát az a feltételezésünk, hogy a valósok felsorolhatók ellentmondásra vezet.
Teljes indukció
A teljes indukció olyan következtetési szabály mely csak matematikai környezetben érvényes.
- Kezdő lépés – igazoljuk, hogy 0-ra teljesül A, azaz az aritmetikában bizonyítható A(0)
- Indukciós lépés – feltesszük, hogy egy tetszőleges n természetes számra igaz és bebizonyítjuk, hogy ezesetben a rákövetkezőjére, azaz n + 1-re is igaz lesz A. Tehát belátjuk, hogy az aritmetikában tétel a (∀n)(A(n) ⇒ A(n+1)) kijelentés.
Példa. Igazoljuk, hogy az első n természetes szám összege n(n+1)/2.
Ehhez egy olyan formális leírási módot választunk, ami gyakran előfordul sorozatoknál. Ez az összegzés:
Mo. A kezdő elemre: 1=1, teljesül. Tegyük föl, hogy igaz az n számra. Tudjuk tehát:
Kell:
3. Feladat. Igazoljuk, hogy minden n természetes számra: n<2n.
Mo. n=1-re teljesül. Tegyük fel, hogy valamely n-re n<2n. Kell, hogy
most szorozzuk be az indukciós feltételt 2-vel:
Ezt fogjuk felhasználni:
4. Feladat (Az összegzés tulajdonságai)
Mo. 3-as: n=1-re teljesül. Indukciós eset. Kell:
Sorozatok
Bevezetés
Végtelen halmazok (valós számok, geometriai ponthalmazok, függvényhalmazok, egyéb végtelen sokaságok) vizsgálatánál gyakran adódik, hogy egy kívánt értéket, tulajdonságot nem kapunk meg egyetlen véges eljárás alkalmazásával egyetlen eredményként. Sokszor egyre mélyebb és mélyebb vizsgálatok eredményezik a pontos értéket. Gyakran az is előfordul, hogy a voltaképpeni végeredmény csak egy végtelen hosszú eljárássorozat végrehajtásával kerülhetne a kezünkbe – feltéve, hogy a végtelen hosszú eljárássorozatot egyáltalán végre tudnánk hajtani.
Példa: a kör
A kör kerületének és átmérőjének viszonyszámának meghatározásakor, azaz a π értékének kiszámításánál is ez a helyzet. Nyilván ez az érték 3 és 4 közé esik, és ha 0,5-es hibán belül megelégszünk az értékével, a 3 jó közelítésnek vehető. További vizsgálatokkal, a körbe írt és a körülírt sokszögek kerületének és átlóinak vizsgálatával ezt az eredményt akár 0,1-es hibahatár alá is szoríthatjuk, mondjuk 3,14-re. További – egyre hosszadalmasabb – számítások elvezethetnek a 3,1415±0,01 értékhez is. Elméleti vizsgálatok kiderítették, hogy a π pontos értékét csak végtelen nemszakaszos tizedestört írja le, így arra esélyünk sincs, hogy az értékeket egyetlen papírlapon láthatjuk leírva. Ellenben, és pontosan ilyen vizsgálatokat jelent a numerikus sorozatok témaköre, igazolható, hogy vannak képletek, melyek segítségével akármilyen előre megadott hibahatár esetén a határon belül kiszámítható a közelítő értéke. Például ilyen képletet adott Leibniz, legalább is a π/4-re
Ekkor az újabb és újabb tagok hozzáadásával keletkező
számsorozatról, azt mondjuk, „tart a π-hez” vagy „konvergál a π-hez” vagy „konvergens és határértéke a π”.
Ugyanígy találhatunk a 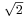 -höz tartó sorozatot. Van olyan is, mely egy görbevonalú síkidom területének mérőszámához, például a parabolacikk területéhez tart.
-höz tartó sorozatot. Van olyan is, mely egy görbevonalú síkidom területének mérőszámához, például a parabolacikk területéhez tart.
Természetesen a feladatunk nem ilyen közelítő képletek készítése lesz. Annak a kérdésnek az általános elméletét tekintjük át, hogy egy akárhogyan megadott sorozat tart-e valamely számhoz, és ha igen, melyikhez.
Definíció
Magán egy számsorozaton olyan hozzárendelést értünk, mely minden pozitív egész számhoz egy számot rendel.
Definíció. Legyen s olyan függvény, melynek értelmezési tartománya Z+ a pozitív egész számok halmaza, értékkészlete pedig egy tetszőleges H halmaz:
ekkor s-et H-beli sorozatnak nevezzük. Ha s értékeit a valós számok halmazából kapja (s:Z+ R), akkor az s sorozat számsorozat vagy numerikus sorozat (numerikus sorozatoknak nevezzük a komplex értékű s:Z+
R), akkor az s sorozat számsorozat vagy numerikus sorozat (numerikus sorozatoknak nevezzük a komplex értékű s:Z+ C sorozatokat is). Jelölésére van egy másik mód is. Ha n pozitív természete szám, akkor a sorozat n számon felvett értékét, vagyis n-edik tagját
C sorozatokat is). Jelölésére van egy másik mód is. Ha n pozitív természete szám, akkor a sorozat n számon felvett értékét, vagyis n-edik tagját
- sn
-nel jelöljük. A teljes egész sorozatot pedig a zárójeles
- (sn)
jelöléssel. Ekkor tehát s = (sn). Egy újabb jelölés, mely szemléletes, de sok helyet foglal és nehéz képletbe foglalni:
- (s1, s2, ..., sn, ...)
(Az értékek lehetnek páronként különbözők is, ekkor a sorozatot még felsorolásnak is nevezzük.)
Példa
Képlettel
Világos, hogy ekkor a sorozat:
Eljárással: a négyzetgyök kettő közelítése intervallumfelezéssel
Ismert az a tény, hogy a kettő négyzetgyöke nem racionális szám (holott helye a számegyenesen körző és vonalzó használatával pontosan kijelölhető). Nincs véges vagy végtelen szakaszos tizedestört előállítása, a tizedestörtben kifejezett értékét csak bizonyos jegyre pontosan tudjuk megmondani. Tudjuk azt is, hogy a racionális számok a számegyenesen mindenhol sűrűn helyezkednek el, azaz bármely két valós szám között van racionális szám. Ez lehetőséget ad arra, hogy megadjunk olyan racionális számokat, melyek egy előre meghatározott távolságnál közelebb vannak a 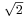 -höz. Tudjuk:
-höz. Tudjuk:
Most osszuk az [1,2] intervallumot két egyenlő részre, határozzuk meg a felezéspont négyzetét és hasonlítsuk össze 2-vel:
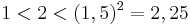
ismételjük az ![[1 ; 1,5]\,](/upload/math/7/b/c/7bc185472fa6d898165440a48daac0d8.png) intervallumra:
intervallumra:
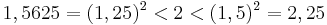
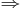

ismételjük az ![[1,25\,;\,1,5]](/upload/math/0/c/1/0c179d58dc6d9e8421372072e7fa123b.png) -re:
-re:

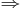

ismételjük az ![[1,375\,;\,1,5]](/upload/math/3/7/e/37ecf12e25881a2a40f2ff6a216d8078.png) -re:
-re:
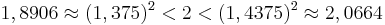
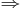
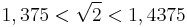
majd az ![[1,375\,;\,1,4375]](/upload/math/b/b/5/bb5d8186ede8e209ce9c8a952b4c74d6.png) -re:
-re:
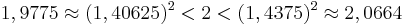
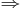
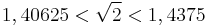
amivel 5 lépésben megkaptuk, hogy a 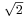 értéke 1 tizedesjegyre
értéke 1 tizedesjegyre 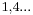 (illetve
(illetve 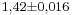 ). Az intervallumok hosszai feleződtek (a
). Az intervallumok hosszai feleződtek (a 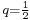 arányú mértani sorozat szerint csökkennek), így az 5. lépésben a keresett érték az intervallum középpontjától már csak
arányú mértani sorozat szerint csökkennek), így az 5. lépésben a keresett érték az intervallum középpontjától már csak 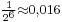 -del tér el. Az eljárásban a
-del tér el. Az eljárásban a 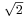 -t alulról és felülről becslő értékek sorozata egy-egy, a
-t alulról és felülről becslő értékek sorozata egy-egy, a 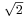 -t közelítő sorozat:
-t közelítő sorozat:
Aki nem jutott volna arra a szubjektív meggyőződésre, hogy az n = 0-ról induló
mértani sorozat egy tag után minden előre megadott kis pozitív számnál kisebb értékeket vesz fel, az gondoljon a
sorozatra (melynek tizedes alakja megegyezik az előző sorozat kettedes tört alakban megadott alakjával) és hogy ez tényleg minden pozitív szám alá megy.
A parabolaszelet területének meghatározása
Geometriai példát is hozhatunk a közelítés alkalmazására. Apollóniuszhoz nyúlik vissza az a módszer, ahogy a parabolametszet területét számítjuk ki.
- Tekintsük a koordinátasíkon az
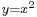 egyenletű parabolát! Határozzuk meg az y = 1 egyenes és a parabolaív által közbezárt terület nagyságát!
egyenletű parabolát! Határozzuk meg az y = 1 egyenes és a parabolaív által közbezárt terület nagyságát!
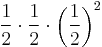 ,
,
négy ilyen van, tehát:
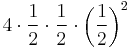 .
.
Ha felezéssel folytatjuk ezt az eljárást, akkor az n-edik lépésben a hozzáadott terület:
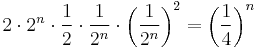 ,
,
így a terület:
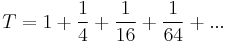 .
.
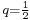 kvóciensű mértani sorozat tagjainak összege, amikor az összes tagot adjuk össze, azaz az
kvóciensű mértani sorozat tagjainak összege, amikor az összes tagot adjuk össze, azaz az
összeg – akármilyen furcsa is – véges érték. (Hogy mit is kell értsünk végtelen tagú összegen, azzal nem is olyan sokára részletesen fogunk foglalkozni.) Az értéke az ábráról – amelyben rendre 1, 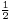 ,
, 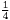 , ... területű téglalapok vannak úgy elrendezve, hogy az összterületük 2 területű téglalap legyen – leolvasható. Általános képletet is ismertek a mértani sorozat tagjainak végtelen összegére (ezt később mi magunk is be tudjuk majd bizonyítani):
, ... területű téglalapok vannak úgy elrendezve, hogy az összterületük 2 területű téglalap legyen – leolvasható. Általános képletet is ismertek a mértani sorozat tagjainak végtelen összegére (ezt később mi magunk is be tudjuk majd bizonyítani):
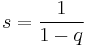 ,
,
így 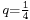 esetén a parabolaszelet területe:
esetén a parabolaszelet területe:
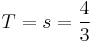 .
.