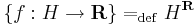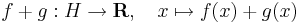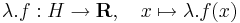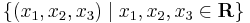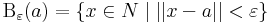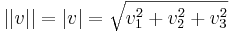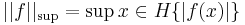Matematika A2a 2008/1. gyakorlat

A MathWikiből

(Változatok közti eltérés)

A lap 2010. február 9., 23:32-kori változata

Ez az szócikk a Matematika A2a 2008 alszócikke.

Függvénytér

A félév során gyakran fogunk találkozni olyan lineáris terekkel (a lineáris tér fogalmát az előadáson tanuljuk meg), melyek elemi függvények. Ezeknek alaptípusa a következő. Legyen H tetszőleges halmaz. Ekkor a

$\{f:H\to \mathbf{R}\}=_\mathrm{def}H^\mathbf{R}\,$

halmazt, azaz a H-n értelmezett R-be képező függvények halmazát függvénytérnek nevezzük. A függvénytér lineáris tér a pontonként műveletekkel, azaz a következőkkel:

$f+g:H\to \mathbf{R},\quad x\mapsto f(x)+g(x)\,$

ha λ valós szám, akkor

$\lambda.f:H\to \mathbf{R},\quad x\mapsto \lambda.f(x)\,$

Függvénytér lineáris alterét is függvénytérnek nevezzük. Lineáris altér egy lineáris tér részhalmaza, ha a fenti műveletekre zárt.

Az F függvénytér B részhalmaza bázis, ha B-beli elemek lineáris kombinációjával a tér összes eleme egyértelműen előáll, azaz ha minden f ∈ F-re léteznek egyértelműen olyan λ₁, ..., λ_n számok, hogy

f = λ 1

f 1

+

λ 2

f 2

+ ...+

λ n

f n

,

ahol f₁, ..., f_n ∈ B. B elemszáma a dimenzió. A lineáris tér egy részhalmaza altér, ha zárt az összeadásra és a számmal való szorzásra.

Példák

1.

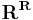$\mathbf{R}^{\mathbf{R}}$ ,

melynek elemeit koordinátarendszerben is tudjuk ábrázolni. Természetesen ez végtelen dimenziós.

2. Az intervallumon korlátos függvények B(I) halmaza altere az előzőnek.

3. A zárt intervallumon folytonos függvények C[a,b] tere része az a B[a,b]-nek. Ugyanígy a Riemann integrálható függvények is R[a,b]

4. Legyen H = {1,2,3}. Ekkor az {f:H $\to$ R} halmazt még úgy is meg lehet adni, hogy az elemeit egy rendezett hármasba foglaljuk:

$\{(x_1,x_2,x_3)\mid x_1,x_2,x_3\in\mathbf{R}\}$

Ezt jelöljük R³-nak. R³ minden elemét meg lehet adni 3 előre megadott elem lineráis kombinációjaként: (1,0,0), (0,1,0), (0,0,1). Ezek alkotják R³ sztenderd bázisát (rendes bázis). Általában Rⁿ. Ebbeli függvények analíziséve fogunk foglalkozni.

5. Legyen R^2×3 a 2-szer 3-as mátrixok tere. Ez szintén lineáris tér az elemenkénti összeadással és a skalárral szorzással. A bázisa 6 elemű.

6. {s:Z $\to$ R} a sorozatok (vagy a polinomok tere). Ez végtelen dimenziós és a báziselemek a hatványfüggvények.

Normált tér

Ha a V vektortéren értelmezünk egy

||.||: V $\to$ R

úgy, hogy

||v|| 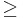$\geq$ 0 minden v ∈ V-re és v=0, ha ||v|| = 0.
minden λ számra és v ∈ V-re |λ| $\cdot$ ||v||=||λ.v||
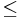||u + v|| $\leq$ ||u|| + ||v||

Hossz azért kell, mert fontos az analítis számára a gömbi környzet, mely, azaz az ε > 0 sugarú a ∈ N középpontú nyílt gömb:

$\mathrm{B}_{\varepsilon}(a)=\{x\in N\mid ||x-a||< \varepsilon\}$

Példa. A főpéldán, az R³-en, ez az euklideszi vektorhossz, azaz a Pithagorasz-tételből kiszámítható

$||v||=|v|=\sqrt{v_1^2+v_2^2+v_3^2}$

Példa. Két lényeges Rⁿ-beli norma.

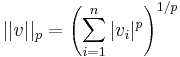
p>0, akkor $||v||_p=\left(\sum\limits_{i=1}^n |v_i|^p\right)^{1/p}$
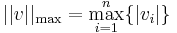
$||v||_{\mathrm{max}}=\max\limits_{i=1}^n\{|v_i|\}$

Érdemes megnézni, hogy a gömbök R²-ben hogy néznek ki. ||.||₁ esetén a gömb egy csúcsára állított négyzet 2 ε átlóval. ||.||_max egy oldalára állított négyzet. ||.||₂pedig egy körlap.

Példa. Függvénytéren a leggyakoribb norma a szuprémumnorma. Ha B(H,R) a H $\to$ R korlátos függvények tere, akkor ennek akármilyen alterén norma az

$||f||_{\mathrm{sup}}=\sup\limits{x\in H}\{|f(x)|\}$

Fontos példák: B[a,b] valóban vektortér, C[a,b] ⊆ B[a,b] altér a Weierstrass-tétel szerint, R[a,b] ⊆ B[a,b] szintén altér amiatt, hogy integrálható függvény korlátos.

2. gyakorlat

@@ 24. sor: / 24. sor: @@
 '''3.''' A zárt intervallumon folytonos függvények C[a,b] tere része az a B[a,b]-nek. Ugyanígy a Riemann integrálható függvények is R[a,b]
-'''4.'''
+'''4.''' Legyen H = {1,2,3}. Ekkor az {f:H <math>\to</math> '''R'''} halmazt még úgy is meg lehet adni, hogy az elemeit egy rendezett hármasba foglaljuk:
+:<math>\{(x_1,x_2,x_3)\mid x_1,x_2,x_3\in\mathbf{R}\}</math>
+Ezt jelöljük '''R'''<sup>3</sup>-nak. '''R'''<sup>3</sup> minden elemét meg lehet adni 3 előre megadott elem lineráis kombinációjaként:
+(1,0,0), (0,1,0), (0,0,1). Ezek alkotják  '''R'''<sup>3</sup> sztenderd bázisát (rendes bázis). Általában '''R'''<sup>n</sup>. Ebbeli függvények analíziséve fogunk foglalkozni.
-<!-- Az első gyakorlaton a '''R'''<sup>n</sup> topologikus tulajdonságait beszéljük meg, különös tekintettel, az '''R'''<sup>n</sup> egy részhalmazából '''R'''<sup>m</sup>-be ható folytonos leképezésekre. A meghatározottság kedvéért '''R'''<sup>n</sup>-en a
+'''5.''' Legyen '''R'''<sup>2&times;3</sup> a 2-szer 3-as mátrixok tere. Ez szintén lineáris tér az elemenkénti összeadással és a skalárral szorzással. A bázisa 6 elemű.
-:<math>\left\{\begin{pmatrix}x_1\\x_2\\\vdots\\x_n\end{pmatrix}:x_1,x_2,...,x_n\in \mathbf{R}\right\}</math>
-halmazt, azaz az n emeletes valós értékű oszlopvektorkat értjük. (Mások azt mondanák, hogy '''R''' saját magával vett n-szeres Descartes-szorzata, ami azonban később elfedné a "sorvektor" és az "oszlopvektor" különbséget, ami a lineáris algebra szempontjából nem kerülendő.)
-Amivel foglalkozunk -- vázlatosan -- azok a következő struktúrák:
+'''6.''' {s:'''Z''' <math>\to</math> '''R'''} a sorozatok (vagy a polinomok tere). Ez végtelen dimenziós és a báziselemek a hatványfüggvények.
-* vektortér: (V, +,  &lambda;._)<sub>&lambda;&isin; '''R'''</sub> azaz a vektorok, ahol tehát van az elemek köztük "összeadás" és valós számmal történő szorzás
-* normált tér: N = (V, ||.||) azaz, ahol már vektorok "hosszát" is értelmezzük
-* euklideszi tér: E = (V, <math>\cdot</math>)  , azaz ahol van "skaláris szorzás" és ebből származtatható a vektorhossz.
-* topológia N felett azaz a környzet és nyilt halmazok fogalma normált téren
-==Lineáris tér==
-Volt '''R'''<sup>3</sup> vektorgeometriájában, hogy a vektorok összadása és skalárral (valós számmal) való szorzása komponensenként történik. A továbbiakban egy magasabb nézőpontból az összeadásnak és a számmal való szorzásnak kiemelünk néhány tulajdonságát és elfeledkezünk arról, hogy ezeknek mi volt a konkrét definíciója. Ezután olyan halmazokat és műveleteket keresünk, melyek esetén a kiemelt "képletek" teljesülnek. A kiemelt tulajdonságok lányegében azok lesznek, hogy az összeadás "valóban" összeadásként viselkedik, a szorzás pedig "valóban" szorzásként.
-Az L halmaz lineáris tér a +:''L''&times;''L'' <math>\to</math> ''L'' összeadással és .:'''R'''&times;''L''<math> \to</math> ''L'' valós számmal szorzással, ha létezik L-ben egy 0 elem és minden L-beli x-hez olyan (-x) szintén L-beli elem, hogy teljesülnek a következő tuljadonságok:
-# x + y = y + x
-# (x + y) + z = x + (y + z)
-# 0 + x = x + 0 = x
-# (-x) + x = x + (-x) = 0
-# &lambda;.(&mu;.x) = (&lambda;&mu;).x
-# &lambda;.(x + y) = &lambda;.x + &mu;.y
-# (&lambda;+&mu;).x = &lambda;.x + &mu;.x
-# 1.x = x
-minden x,y L-belire és &lambda;, &mu; '''R'''-belire. Az ilyet valós test feletti lineáris térnek, vagy vektortérnek is nevezik.
-Két lényeges fogalom. Lineáris kombináció:
-:<math>\lambda_1</math><math>x^1</math> + <math>\lambda_2</math><math>x_2</math> + ...+ <math> \lambda_n</math><math>x_n</math>.
-Dimenzió: hány előre megadott vektor lineáris kombinációjából áll elő egyértelműen a tér bármely vektora. Ez utóbbi fogalmat persze még erősen finomítani kell.
-===Példák===
-'''1.'''  Az '''R'''<sup>n</sup> oszlopvektorok vagy az '''R'''<sup>1&times;n</sup> sorvektorok tere a koordinátánkénti összeadással ill. skaláris szorzással. De ugyanígy az m&times;n-es táblázatok, azaz mátrixok '''R'''<sup>m&times;n</sup> tere vektortér. ('''R'''<sup>n</sup> azért fontos, mert az összes véges dimenziós vektortér izomorf vele.)
-'''2.''' Akármilyen H nemüres halmaz és az {f: H <math>\to</math> '''R'''} függvények halmaza vektortér az (<math>f_1</math> + <math>f_2</math>)(x) := <math>f_1</math>(x) + <math>f_2</math>(x)  (x&isin; H) pontonkénti összeadással és a(&lambda;<math>f</math>)(x) := &lambda;<math>f_1</math>(x)   (x&isin; H) pontonkénti szorzással. (Például homogén lineáris diffegyenletek megoldásai, azaz bizonyos függvények vektorteret alkotnak.)
-'''3.''' Érdekes terek a sorozatterek illetve a polinomok lineáris tere. Az összes <math>a_0</math> + <math>a_1</math> <math>x</math> + <math>a_2</math> <math>x^2</math> + ... +<math> a_n</math><math>x^n</math> polinomok halmaza lineáris teret alkot. Ez egy végtelen dimenziós vektortér.
-Tulajdonképpen mindegyik eddig ismertetett példa függvénytér. 1.-ben H = {1,2,...,n} az '''R'''<sup>n</sup>-et generálja, vagy az {1,2,...,n} &times; {1,2,...,n} a mátrixok  '''R'''<sup>n&times;n</sup> halmazát. 3.-ban H = '''Z'''<sup>+</sup> és a példa az ezáltal generált tér egy altere.
 ==Normált tér==
@@ 91. sor: / 59. sor: @@
 :<math>||f||_{\mathrm{sup}}=\sup\limits{x\in H}\{|f(x)|\}</math>
 Fontos példák: B[a,b] valóban vektortér, C[a,b] &sube; B[a,b] altér a Weierstrass-tétel szerint, R[a,b] &sube; B[a,b] szintén altér amiatt, hogy integrálható függvény korlátos.
+<!--
 ==Euklideszi terek==
 Csak megjegyezzük, hogy ha egy vektortéren be lehet vezetni skaláris szorzatot, abban az értelmeben, ahogy az a top.pdf-en le van írva, akkor rögvest eljutunk a normához.

Matematika A2a 2008/1. gyakorlat

A lap 2010. február 9., 23:32-kori változata

Függvénytér

Példák

Normált tér

Nézetek

Személyes eszközök

Navigáció

Keresés

Eszközök