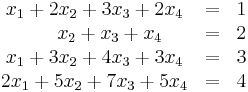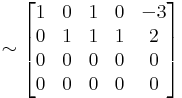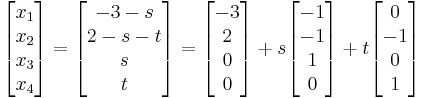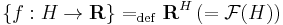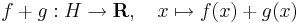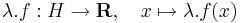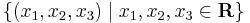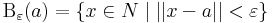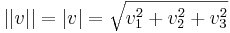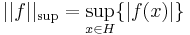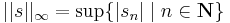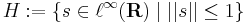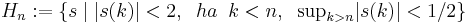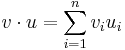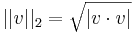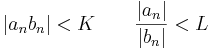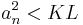Matematika A2a 2008/1. gyakorlat
- Ez az szócikk a Matematika A2a 2008 alszócikke.
Tartalomjegyzék |
Többváltozós bemelegítés
Oldja meg az
egyenletrendszert!
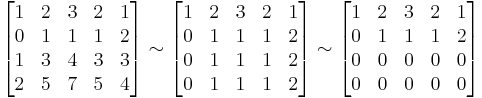
MO. A kibővített mátrix:
Ez utóbbit hívják lépcsős alaknak. Ha most a főátlóba egyeseket teszünk (vezérelemek) és fölöttük alattuk csak nullák állnak (a többi maradhat), akkor a redukált lépcsős alakhoz jutunk.
Innen a megoldás (az x3 és x4 változókat rendre az s és t paramétereknek választva)
Függvénytér
A félév során gyakran fogunk találkozni olyan lineáris terekkel (a lineáris tér fogalmát az előadáson tanuljuk meg), melyek elemei függvények. Ezeknek alaptípusa a következő. Legyen H tetszőleges halmaz. Ekkor a
halmazt, azaz a H-n értelmezett R-be képező függvények halmazát függvénytérnek nevezzük. A függvénytér lineáris tér a pontonként műveletekkel, azaz a következőkkel:
ha λ valós szám, akkor
Függvénytér lineáris alterét is függvénytérnek nevezzük. Lineáris altér egy lineáris tér részhalmaza, ha a fenti műveletekre zárt.
Feledat. a) Keressünk olyan n ∈ F(H)-t, melyre minden f esetén n+f=f+n=f! b) Keressünk minden f ∈ F(H)-hez olyan g-t, melyre az előző (egyébként egyértelmű) n ∈ F(H)-nel f+g=g+f=n teljesül! c) Igazoljuk, hogy minden f, g ∈ F(H)-re λ(f + g) = λf + λg, (λ + μ)f = λf + μf, λ(μf) = (λμ)f, 1.f = f!
Az F függvénytér B részhalmaza bázis, ha B-beli elemek lineáris kombinációjával a tér összes eleme egyértelműen előáll, azaz ha minden f ∈ F-re léteznek egyértelműen olyan λ1, ..., λn számok, hogy
- f = λ1f1 + λ2f2 + ...+ λnfn,
ahol f1, ..., fn ∈ B. B elemszáma a (véges) dimenzió.
Példák
1.
 ,
,
melynek elemeit koordinátarendszerben is tudjuk ábrázolni. Természetesen ez végtelen dimenziós.
2. Az intervallumon korlátos függvények B(I) halmaza altere az előzőnek.
3. A zárt és korlátos intervallumon folytonos függvények C[a,b] tere része az a B[a,b]-nek. Ugyanígy a Riemann integrálható függvények is R[a,b] tere is.
4. Legyen H = {1,2,3}. Ekkor az {f:H  R} halmazt még úgy is meg lehet adni, hogy az elemeit egy rendezett hármasba foglaljuk:
R} halmazt még úgy is meg lehet adni, hogy az elemeit egy rendezett hármasba foglaljuk:
Ezt jelöljük R3-nak. R3 minden elemét meg lehet adni 3 előre megadott elem lineráis kombinációjaként: (1,0,0), (0,1,0), (0,0,1). Ezek alkotják R3 sztenderd bázisát (rendes bázis). Általában Rn. Ebbeli függvények analíziséve fogunk foglalkozni.
5. Legyen R2×3 a 2-szer 3-as mátrixok tere. Ez szintén lineáris tér az elemenkénti összeadással és a skalárral szorzással. A bázisa 6 elemű.
6. {s:Z  R} azon részhalmaza, mely az egy "idő után konstans nulla" sorozatokból áll (
R} azon részhalmaza, mely az egy "idő után konstans nulla" sorozatokból áll (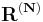 ) (ami azonosítható a polinomok terével). Ez végtelen dimenziós és a báziselemek a hatványfüggvények.
) (ami azonosítható a polinomok terével). Ez végtelen dimenziós és a báziselemek a hatványfüggvények.
Normált tér
Az N vektortéren értelmezett
- ||.||: N
 R
R
függvény norma N-en, ha
- ||v||
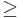 0 minden v ∈ N-re és v=0, ha ||v|| = 0.
0 minden v ∈ N-re és v=0, ha ||v|| = 0.
- minden λ számra és v ∈ N-re |λ|
 ||v||=||λ.v||
||v||=||λ.v||
- ||u + v||
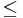 ||u|| + ||v||
||u|| + ||v||
Ekkor N a ||.||-val ellátva normált tér.
Hossz azért kell, mert fontos az analízis számára a gömbi környezet, azaz az ε > 0 sugarú a ∈ N középpontú nyílt gömb:
Példa. A főpéldán, az R3-en, ez az euklideszi vektorhossz, azaz a Pithagorasz-tételből kiszámítható
Példa. Két lényeges Rn-beli norma.
- p>0, akkor
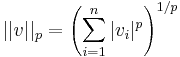
-
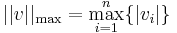
Érdemes megnézni, hogy a gömbök R2-ben hogy néznek ki. ||.||1 esetén a gömb egy csúcsára állított négyzet 2 ε átlóval. ||.||max egy oldalára állított négyzet. ||.||2pedig egy körlap.
Példa. Függvénytéren a leggyakoribb norma a szuprémumnorma. Ha B(H,R) a H  R korlátos függvények tere, akkor ennek akármilyen alterén norma az
R korlátos függvények tere, akkor ennek akármilyen alterén norma az
Topológia
u belső pontja H-nak, ha van olyan (gömbi) környezete u-nak, mely teljes egészében H-beli. H nyílt halmaz, ha minden pontja belső pont. H zárt, ha komplementere, azaz az
halmaz nyílt.
Tétel. Minden véges dimenziós normált tér ekvivalens egymással topologikus szempontból, azaz bármilyik norma ugyanazokat a nyílt halmazokat határozza meg.
Célszerű tehát a feladatokban választani például azt a p-edik normát, mellyel a legkönnyebben lehet számolni.
Világos, hogy Rn nyílt halmaz, így ennek komplementere, az üres halmaz zárt. Ám, az üres halmaz nyílt is, hiszen minden pontja belső pont. Ha ugyanis lenne olyan pontja, ami nem belső pontja, akkor lenne egyáltalán pontja, ami lehetetlen, lévén az üres halmaz üres. Így komplementere, azaz Rn zárt halmaz is. Tanulság: vannak nyílt-zárt halmazok (clopen in English) és vannak se nem nyílt, se nem zárt halmazok, például a [0,1) intervallum. Vagyis "a halmaz nem ajtó, ami vagy nyílt, vagy zárt"!
Véges sok nyílt halmaz metszete nyílt, akármennyi nyílt halmaz uniója nyílt. A zártakra a duális állítás igaz: véges sok zárt halmaz uniója zárt, akárhány zárt halmaz metszete zárt.
- Igazoljuk, hogy végtelen sok nyílt halmaz uniója nyílt!
- Igazoljuk, hogy véges sok nyílt halmaz metszete nyílt!
- Adjuk példát végtelen sok nyílt halmazra, amelyek metszete nem nyílt!
- Adjuk példát végtelen sok zárt halmazra, amelyek uniója nem zárt!
Kiegészítő anyag
Heine--Borel-tételkör
Kompakt egy K halmaz, ha minden nyílt halmazrendszerből, melynek uniója lefedi K-t kiválasztható véges sok nyílt halmaz is, melyek véges uniója még mindig lefedi K-t.
Heine-Borel-tétel. Véges dimenziós normált térben minden korlátos és zárt halmaz kompakt.
Rn véges dimenziószáma nagyon lényegesen hozzájárul a fenti tételek fennállásához. Általában (Haussdorf-térben) kompakt halmaz korlátos és zárt. Ám, van olyan végtelen dimenziós normált tér, melyben zárt és korlátos halmaz nem kompakt. Legyen ugyanis 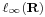 a korlátos sorozatok tere. A téren a norma a suprémum:
a korlátos sorozatok tere. A téren a norma a suprémum:
Példa.
"gömb" zárt, korlátos, de nem kompakt.
Ugyanis, Nyilván korlátos, mert belefoglalható a B2(0) kétség sugarú 0 körüli gömbbe. Zárt is, ehhez nézzük a komplementerét! Ha ||s||> 1, az pontosan azt jelenti, hogy sup s >1, azaz létezik olyan ε>0, hogy minden n-re |s(n)| > 1+ ε. Pozitív s(n)-re vegyük az s(n)>(s(n)+1+ε)/2 > 1+ε, negatív tagokra az s(n)<(s(n)+(-1-epsilon))/2<-1-ε elemekből álló t sorozatot. Ez a komplementerben halad, mert sup |t| > 1+(ε/2).
De nem kompakt. Fedjük le ugyanis a
halmazokkal! Ezek nyíltak, de véges sok nem fedi le H-t.
Hasonló furcsaságok jelentkeznek a p-edik hatványon szummálható sorozatok 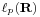 terében is. Számunkra esetleg a véges sorösszeggel rendelkező
terében is. Számunkra esetleg a véges sorösszeggel rendelkező 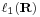 tér bír jelentőséggel.
tér bír jelentőséggel.
Feladatok skaláris szorzásra
Euklideszi terek
Csak megjegyezzük, hogy ha egy vektortéren be lehet vezetni skaláris szorzatot, abban az értelmeben, ahogy az a top.pdf-en le van írva, akkor rögvest eljutunk a normához.
Példa. Ha v,u ∈ Rn, akkor
Ekkor
Példa.
Legyen (an), (bn) : Z+  RN és 0 nem eleme Ran(||bn||). Melyikből következik melyik:
RN és 0 nem eleme Ran(||bn||). Melyikből következik melyik:
- (i)
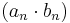 korlátos és
korlátos és 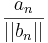 korlátos
korlátos
- (ii) (an) korlátos és (bn) is korlátos
- (iii) (an) korlátos vagy (bn) korlátos
Itt (anbn) a sorozatok elemeinek skaláris szorzatából készített sorozat.
Megoldás
- (i)
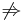 (ii)
(ii)
ugyanis az ellenpélda már R-ben jelentkezik: (an) = (0,0,0,...,0,...) és (bn) = (1,2,3, ...,n,...). Világos, hogy a szorzat és a hányados is korlátos, mert mindkettő az azonosan nulla, holott (bn) az Archimédészi axióma miatt nem korlátos.
- (ii)
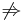 (i)
(i)
Szintén már R-ben jelentkezik az ellenpélda:
mindekettő korlátos, és még a szorzat is, de a hányados már nem.
- (ii)
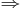 (iii) tisztán logikai okokból
(iii) tisztán logikai okokból
- (iii)
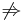 (ii) azt nem állítanám hogy tisztán logikai okokból, de az adott szituációban mindenképpen. Magyarán ellenpélda kell: az egyik a csupanulla, a másik az (n).
(ii) azt nem állítanám hogy tisztán logikai okokból, de az adott szituációban mindenképpen. Magyarán ellenpélda kell: az egyik a csupanulla, a másik az (n).
- (iii)
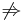 (i) már R-ben sem: csupanulla, (n)
(i) már R-ben sem: csupanulla, (n)
- (i)
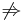 (iii)
(iii)
A legérdekesebb eset. R-ben igaz, magasabb dimenzióban nem, tehát összességében nem. R-ben:
akkor
amiből az egyik, azaz (an) korlátos. De R2-ben már nem igaz: (an) = ((n,0)), (bn) = ((0,n)). Ezek skaláris szorzata 0, az első osztva a második elemenkénti normájával az y irányú egységvektor, mint konstans sorozatot adja.
| 2. gyakorlat |