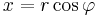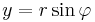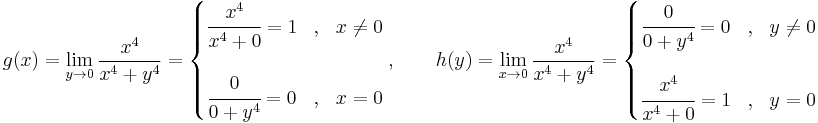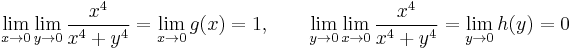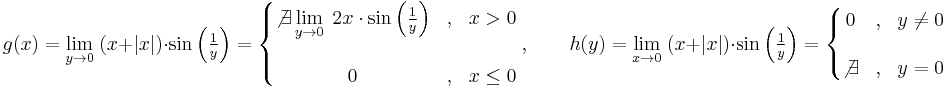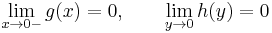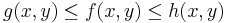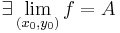Matematika A2a 2008/2. gyakorlat
Mozo (vitalap | szerkesztései) (→Határérték) |
Mozo (vitalap | szerkesztései) (→Határérték) |
||
| 58. sor: | 58. sor: | ||
:minden ε>0-ra létezik δ>0, hogy <math>f\left(\dot{\mathrm{B}}_\delta(x_0,y_0)\right)\subseteq \mathrm{B}_\varepsilon(A)</math> | :minden ε>0-ra létezik δ>0, hogy <math>f\left(\dot{\mathrm{B}}_\delta(x_0,y_0)\right)\subseteq \mathrm{B}_\varepsilon(A)</math> | ||
Ilyenkor <math>\lim\limits_{(x,y)\to (x_0,y_0)}f(x,y)=A</math>-t vagy <math>\lim\limits_{(x_0,y_0)}f=A</math>-t írunk. | Ilyenkor <math>\lim\limits_{(x,y)\to (x_0,y_0)}f(x,y)=A</math>-t vagy <math>\lim\limits_{(x_0,y_0)}f=A</math>-t írunk. | ||
| + | |||
'''Rendőrelv''' Legyen <math>f,g,h:U\to \mathbf{R}</math> és <math>(x_0,y_0)\in U'</math>. Ha van olyan δ>0, hogy minden <math>(x,y)\in\mathrm{B}(x_0,y_0)\cap U</math>-ra | '''Rendőrelv''' Legyen <math>f,g,h:U\to \mathbf{R}</math> és <math>(x_0,y_0)\in U'</math>. Ha van olyan δ>0, hogy minden <math>(x,y)\in\mathrm{B}(x_0,y_0)\cap U</math>-ra | ||
:<math>g(x,y)\leq f(x,y)\leq h(x,y)\,</math> | :<math>g(x,y)\leq f(x,y)\leq h(x,y)\,</math> | ||
és <math>\exists\lim\limits_{(x_0,y_0)}g=A</math> és <math>\exists\lim\limits_{(x_0,y_0)}h=A</math>, akkor | és <math>\exists\lim\limits_{(x_0,y_0)}g=A</math> és <math>\exists\lim\limits_{(x_0,y_0)}h=A</math>, akkor | ||
:<math>\exists\lim\limits_{(x_0,y_0)}f=A</math> | :<math>\exists\lim\limits_{(x_0,y_0)}f=A</math> | ||
| + | |||
| + | '''Határérték nem létezésének jellemzése.''' Tegyük fel, hogy az <math>f:\mathbf{R^2}\supset\to \mathbf{R}</math> függvény értelmezési tartományának <math>(x_0,y_0)</math> torlódási pontja. <math>f</math>-nek nem létezik határértéke az <math>(x_0,y_0)</math> pontban, pontosan akkor, ha léteznek olyan <math>(\mathbf{x}_n)</math> és <math>(\mathbf{x}_n')</math> sorozatok, hogy <math>\mathbf{x}_n\to (x_0,y_0)</math> és <math>\mathbf{x}_n'\to (x_0,y_0)</math>, de <math>f(\mathbf{x}_n)</math> vagy <math>f(\mathbf{x}_n')</math> nem konvergensek, vagy ha igen, akkor <math>\lim f(\mathbf{x}_n)\ne \lim f(\mathbf{x}_n)</math>. | ||
<!-- | <!-- | ||
==Sorozatok konvergenciája normált térben== | ==Sorozatok konvergenciája normált térben== | ||
A lap 2017. február 12., 22:44-kori változata
- Ez az szócikk a Matematika A2a 2008 alszócikke.
Kétváltozós függvények szemléltetése
a) 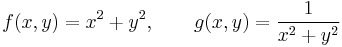
b) 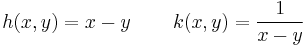
Ezek (x,y,z) koordinátarendszerbeli z=f(x,y) felülettel ábrázolva hengerszimmetrikusak, érdemes az
polárkoordináta transzformációval átírni, ebben 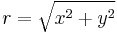 a z-tengelytől mért távolság, és az első és második (majd a második és harmadik síknegyedben):
a z-tengelytől mért távolság, és az első és második (majd a második és harmadik síknegyedben): 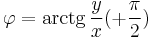
Innen: 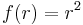 z körül körbeforgatott parabola (forgási paraboloid)
z körül körbeforgatott parabola (forgási paraboloid)
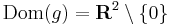 és
és 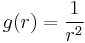 másodfokú hiperbola körbeforgatva.
másodfokú hiperbola körbeforgatva.
Mindkettő szintvonalai körök.
b) h(x,y)=z=x-y egy sík egyenlete, szintvonalai: c=x-y, y=x-c egyenesek.
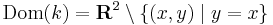 szintén egyenesek a szintvonalak:
szintén egyenesek a szintvonalak: 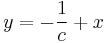 .
.
Iterált határérték
a) 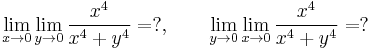
b*) 
c) 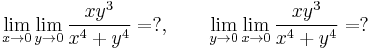
MO.
a)
b)
Tehát g csak a nemnegatívokon értelmezett és ott 0:
*Feladat. a) Ha az iterált határértékek léteznek, de nem egyenlők, akkor a határérték nem létezik. b) Van olyan, hogy az iterált határérték nem létezik, de a határérték igen. c) Van olyan, hogy az iterált határértékek léteznek és egyenlők, de a határérték nem létezik.
Határérték
Def. Tegyük fel, hogy az 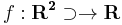 függvény értelmezési tartományának (x0,y0) torlódási pontja. Azt mondjuk, hogy f-nek létezik határértéke az (x0,y0) pontban, és ez az A szám, ha
függvény értelmezési tartományának (x0,y0) torlódási pontja. Azt mondjuk, hogy f-nek létezik határértéke az (x0,y0) pontban, és ez az A szám, ha
- minden ε>0-ra létezik δ>0, hogy
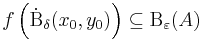
Ilyenkor 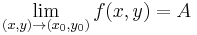 -t vagy
-t vagy 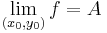 -t írunk.
-t írunk.
Rendőrelv Legyen 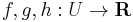 és
és 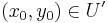 . Ha van olyan δ>0, hogy minden
. Ha van olyan δ>0, hogy minden 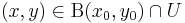 -ra
-ra
és 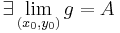 és
és 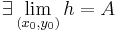 , akkor
, akkor
Határérték nem létezésének jellemzése. Tegyük fel, hogy az 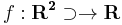 függvény értelmezési tartományának (x0,y0) torlódási pontja. f-nek nem létezik határértéke az (x0,y0) pontban, pontosan akkor, ha léteznek olyan
függvény értelmezési tartományának (x0,y0) torlódási pontja. f-nek nem létezik határértéke az (x0,y0) pontban, pontosan akkor, ha léteznek olyan 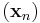 és
és 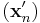 sorozatok, hogy
sorozatok, hogy 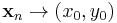 és
és 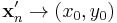 , de
, de 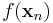 vagy
vagy 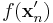 nem konvergensek, vagy ha igen, akkor
nem konvergensek, vagy ha igen, akkor 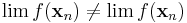 .
.
| 1. gyakorlat | 3. gyakorlat |