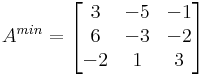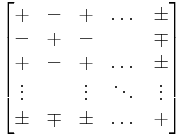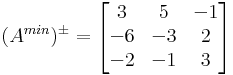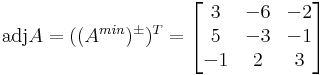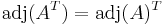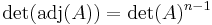Adjungált
- Ez a szócikk a mátrixok inverzének kiszámításánál szereplő adjungált mennyiségről szól, vagyis a „klasszikus adjungáltról”. A komplex algebra adjungáltfogalma, vagyis a konjugált transzponáltat máshol kell keresni.
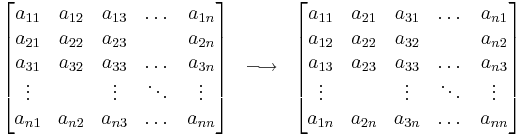
A lineáris algebrában egy négyzetes mátrix adjungáltjának nevezzük a mátrix előjeles aldeterminánsaiból alkotott mátrix transzponáltját. Az adjungálás tehát a négyzetes mátrixokon értelmezett operáció, mely mátrixhoz mátrixot rendel. Legfontosabb alkalmazása, hogy segítségével tömör formában fejezhető ki egy invertálható mátrix inverze.
Tartalomjegyzék |
Definíció
Egy A kvadratikus (négyzetes, azaz n×n-es) mátrix adjungáltján a következő eljárással elkészített mátrixot értjük:
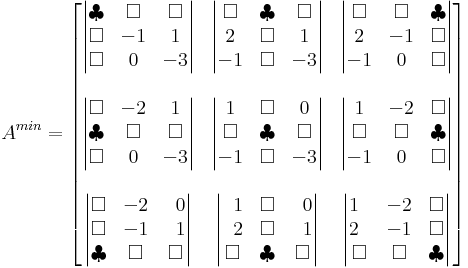
- felírjuk az A mátrix aldeterminánsmátrixát vagy minormátrixát, vagyis azt az Amin mátrixot, melynek i,j-edik eleme annak a mátrixnak a determinánsa, melyet az A i-edik sorának és j-edik oszlopának törlésével keletkezik;
- az Amin mátrix elemeinek előjelét a „sakktáblaszabály” szerint megváltoztatjuk, azaz az i,j-edik elemnek a (−1)i+j értéket adjuk, ekkor nyerjük az előjeles aldeterminánsmátrixot, azaz a (Amin)± mátrixot;
- majd ezt a mátrixot transzponáljuk, azaz elemeit a főátlóra tükrözzük: ((Amin)±)T
Így kapjuk az
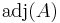 -val
-val
jelölt adjungált mátrixot.
Az adjungált mátrix definíciójának értelmét az inverz mátrix kiszámítására vonatkozó tétel bizonyításában keressük!
Példa
Legyen A a következő négyzetes mátrix:
Aldetermináns-mátrix
Készítsük el az aldeterminánsmátrixot, azaz a minormátrixot! Az Amin mátrix elemeit – a  helyen álló elemet – tehát úgy kapjuk az A elemeiből, hogy az i-edik sort és j-edik oszlopot törtöljük (ezek a
helyen álló elemet – tehát úgy kapjuk az A elemeiből, hogy az i-edik sort és j-edik oszlopot törtöljük (ezek a  helyek) és a maradék mátrix determinánsát számítjuk ki. Az aldetermináns mátrix elemei a következő determinánsok lesznek:
helyek) és a maradék mátrix determinánsát számítjuk ki. Az aldetermináns mátrix elemei a következő determinánsok lesznek:
Tehát a 2×2-es determinánsok kiszámítása után:
Előjeles aldetermináns-mátrix
A „sakktáblaszabály” alapján a következő formális mátrix mutatja, hogy hol kell megváltoztatni az előjelet (–) és hol nem (+)
Tehát
Transzponált
A transzponálás, a mátrix elemeinek a főátlóra történő tükrözése – az első sorból lesz az első oszlop, a második sorból a második oszlop, ... Tetszőleges kvadratikus mátrixnál tehát ez az operáció:
Így az adjungált:
Adjungált-képlet
A Caley–Hamilton-tétel következményeként egy mátrix gyöke saját karakterisztikus polinomjának. Ezekben a polinomokban a konstans tag mindig a mátrix determinánsa, így (invertálható esetben) az inverzmátrixal történő beszorzás után, ebből a konstans tagból a det(A) A-1 = adj(A) mátrixot kapjuk. A karakterisztikus egyenlet változójának helyére az A mátrixot helyettesítve és az inverzel beszorozva tehát kifejezhető az adjungált. Sőt, ez az így nyert formula szinguláris mátrix esetén is fennáll. Ez a formula a 2×2-es esetben:
A-1 = adj(A) mátrixot kapjuk. A karakterisztikus egyenlet változójának helyére az A mátrixot helyettesítve és az inverzel beszorozva tehát kifejezhető az adjungált. Sőt, ez az így nyert formula szinguláris mátrix esetén is fennáll. Ez a formula a 2×2-es esetben:
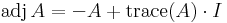 ,
,
a 3×3-as esetben pedig
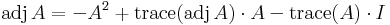 .
.