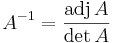Inverz mátrix

Egy reguláris mátrix inverze olyan mátrix, mellyel őt jobbról balról beszorozva egységmátrixot kapunk.

Inverz mátrix képlet

Egy invertálható A mátrix esetén az A^-1 inverz a következőképpen írható fel:

$A^{-1}=\frac{\mathrm{adj}\,A}{\mathrm{det}\,A}$

itt adj A az A adjungáltja, a det A számmal való osztás az A invertálhatósága miatt elvégezhető, hiszen ekkor ez nem nulla.

Bizonyítás. Elég belátni, hogy

A $\cdot$ adj(A) = det(A)$\cdot$I,

ahol I az egységmátrix. Ha az előjeles aldetermináns-mátrix értékeit ±M_ji-vel jelöljük (a minormátrix megfelelő előjellel ellátott transzponáltja), akkor a mátrixszorzat szokásos táblázatos ábrázolásában a következő egyenlőséget kell igazolnunk:

$\begin{matrix} & \begin{bmatrix} +M_{11}&-M_{21}&+M_{31}&\dots&\pm M_{n1}\\ -M_{12}&+M_{22}&-M_{32}& &\mp M_{n2}\\ +M_{13}&-M_{23}&+M_{33}&\dots&\pm M_{n3}\\ \vdots& &\vdots&\ddots&\vdots\\ \pm M_{1n}&\mp M_{2n}&\pm M_{3n}&\dots&+M_{nn} \end{bmatrix}\\\\ \begin{bmatrix} a_{11}&a_{12}&a_{13}&\dots&a_{1n}\\ a_{21}&a_{22}&a_{23}& &a_{2n}\\ a_{31}&a_{32}&a_{33}&\dots&a_{3n}\\ \vdots& &\vdots&\ddots&\vdots\\ a_{n1}&a_{n2}&a_{n3}&\dots&a_{nn} \end{bmatrix} & \begin{bmatrix} \mathrm{det}\,A\; &0&0&\dots&0\\ 0&\mathrm{det}\,A\;&0& &0\\ 0&0&\mathrm{det}\,A\;&\dots&0\\ \vdots& &\vdots&\ddots&\vdots\\ 0&0&0&\dots&\mathrm{det}\,A\; \end{bmatrix} \end{matrix}$

Az adjungált pont úgy lett megszerkesztve, hogy pontosan illeszkedjék a determinánsok kifejtési tételéhez (illetve a ferde kifejtési tételhez). Ha az A i-edik (a_i1,a_i2,a_i3,...,a_in) sorát az adjungált i-edik ((-1)ⁱ⁺¹M_i1,(-1)ⁱ⁺²M_i2,(-1)ⁱ⁺³M_i3,...,(-1)ⁱ⁺ⁿM_in) oszlopával szorzunk, akkor pont azokat az elemeket kell egymással összeszorozni, amely szorzatoknak az összege a kifejetési tételben a determinánst adja. Ezért a szorzat i,i-edik eleme, azaz tetszőleges főátlóbeli elem maga az A determinánsa lesz. A ferde kifejtési tétel szerint a determinánst úgy fejtve ki, hogy egy sort a nem hozzá tartozó „aldetermináns-oszloppal” szorzunk be, mindig 0-t kapunk, azaz a főátlón kívül csupa 0 lesz. QED■